| The outer or Irregular moons of Saturn were my primary research topic during the 2nd half of the Cassini mission at Saturn. This website gives an overview, including links to individual-moon pages. | Die sogenannten irregulären oder äußeren Monde von Saturn waren mein primäres Forschungsthema während der zweiten Hälfte der Cassinimission am Saturn. Diese Seite gibt eine Übersicht (auf englisch). |
The outer or Irregular moons of Saturn represent a distinct class of objects in the solar system. So far, orbits of 122 individual objects are known, but there exist a lot more. They differ from the 24 known inner or regular satellites of Saturn because their orbits are much larger, in most cases highly inclined and elliptical, and they are significantly disturbed by the gravity of the Sun. Saturn’s Irregulars are way more numerous than the regular moons, occupy a much larger volume within the gravitational field of the planet, and are mainly found on retrograde orbits (current count: prograde 22; retrograde 💯). Most “Irregulars” are quite small: Only Phoebe (diameter 213 km) is a modestly large object, while all others are smaller than ∼40 km and mostly even below 10 km (the smallest ones have diameters of ∼2¼ km). Their revolution periods around Saturn range from ∼1¼ to ∼4½ years, the mean distances to Saturn from ∼11 million to more than 26 million km, and the known rotation periods from ∼¼ to ∼3 days. The Irregulars are likely collisional remnants of progenitor objects of unclear origin, captured long ago by Saturn through a process that is not well understood. Later mutual collisions are the likely reason why they are so numerous.
 |
Fig. (left): Cassini image of Irregular moon Erriapus, taken on 24 Dec 2016 05:10 UTC from a distance of 10.7 million kilometers. Exposure time was 220 sec, the cross marks the object. Erriapus is much smaller (∼10 kilometers) than the spatial resolution of the image (∼128 kilometers per pixel) (summation mode). The other spots and streaks in the image are background stars or galaxies, or hits of charged cosmic particles on the CCD of the camera. The prominent spiral galaxy is NGC 300 in constellation Sculptor; it is ∼6 million lightyears away from our Solar System. |
 |
Fig. (right): The chapter about Saturn’s Irregular moons in the Enceladus and the Icy Moons of Saturn book from 2018 provides detailed information on this class of Solar-System objects on 26 pages just after the end of the Cassini mission. |
 |
Table of basic orbit and physical properties of Saturn’s Irregular moons (text file). |
This website compiles (much of) our knowledge on Saturn’s Irregular moons in compact form. Its main focus lies on the observations and results that I obtained through the observations with the camera of the Cassini spacecraft. A reference list for more in-depth reading is provided at the last sheet of this page.
This site is permanently under development. As soon as new papers or other information related to the topic will become available, content will be added.
Last update: 23 Feb 2024 — page content is best displayed on a screen at least 1024 pixels wide
(1) Links to individual Irregular-moon pages
Basic astronomical and physical properties of Saturn’s Irregular moons as well as Cassini imaging observation planning details are provided on individual websites for each moon.
Notes: A ‘•‘ behind a moon name indicates that this object orbits progradely; all others have retrograde orbits. The prograde moons are listed in the four upper rows. Further orbit-dynamical subdivision of the progrades: ¹: Gallic group member; ²: Inuit group member (dynamically related to: ˢ: Siarnaq; ᴷ: Kiviuq).
An ‘×’ highlights objects with a “record property” like largest/smallest distance to Saturn, orbit eccentricity, inclination, size, rotation period, or lightcurve amplitude.
The nine largest objects are highlighted in yellow (outstanding Phoebe in orange); they have all been observed by the Cassini spacecraft. Sixteen smaller moons which Cassini also observed successfully are marked by a medium-gray background of the tiles; lightcurves of these 25 objects are discussed in Denk and Mottola (2019). For all other Irregulars, no Cassini data exist which show the object. Note that at the time of the Cassini mission (which ended in Sep 2017), only 38 Irregular moons of Saturn have been known (this ‘sheet #1’ would have looked → like this). These are marked in bold.
Besides the moons listed in the table, there exist many more Saturnian Irregular moons with so far unknown orbital elements.
(2) Orbit properties
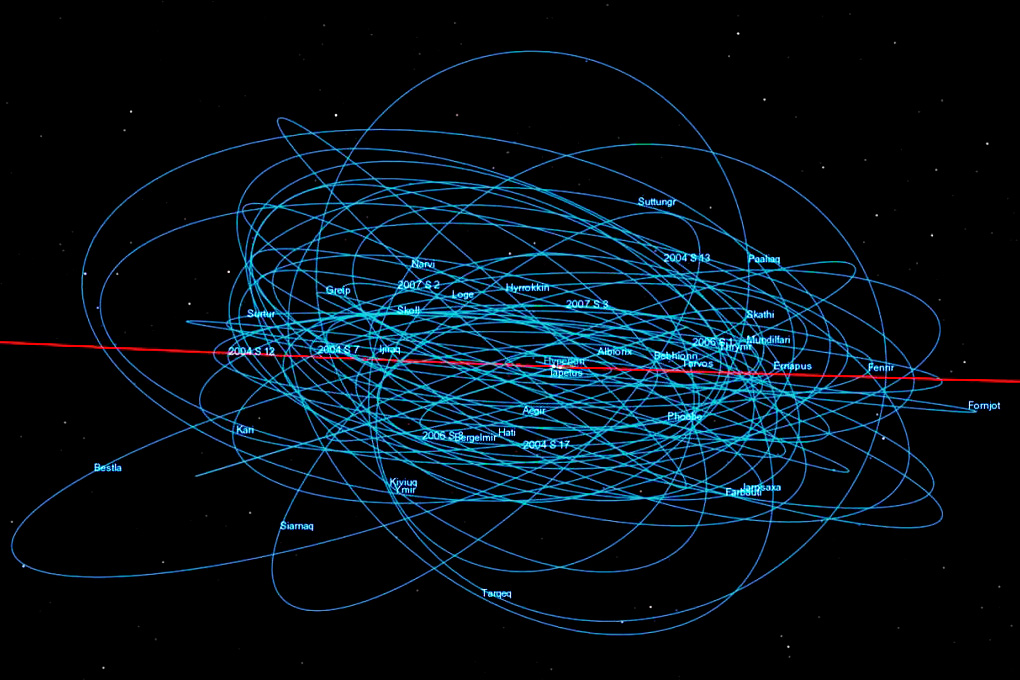The known Irregulars reach ranges to Saturn between 3.7·106 km and 44·106 km. (These numbers reflect potentially extreme periapses of object S/2019 S 1, and the potentially extreme apoapses of S/2004 S 36 within the next couple of thousands of years.) They require between 1¼ (S/2019 S 1; Kiviuq; Ijiraq; S/2020 S 1) and ∼4½ years (Saturn LVIII) for one revolution around Saturn, the respective mean distances (semi-major axes a) are 11.2·106 km and 26.1·106 km. For comparison, Iapetus, the regular satellite farthest from Saturn, has a distance of 3.6·106 km and requires just 0.22 years for one orbit. This means that S/2019 S 1 almost “touches” the Iapetus orbit from time to time. The orbit eccentricities e of Saturn’s known Irregulars vary over the next ∼5000 years from almost zero (S/2020 S 3 and others) to ∼0.80 (S/2004 S 36). Note that the orbits of the regular moons (except for Hyperion) are almost circular (e < 0.03). The inclinations i of the Irregulars diverge between ∼28° and ∼58° (prograde moons Tarvos and S/2019 S 1) and between ∼145° and ∼180° (retrograde moons Bestla and Alvaldi).
The discrimination into objects with prograde and retrograde motions about Saturn in planetocentric coordinates is a fundamental classification of Irregular moons. To date, 22 objects on prograde and 100 on retrograde orbits are known. Furthermore, many of the moons cluster around similar a,e,i values and are thus possibly parts of “dynamical families”. Figure 2A shows the “orbital architecture” of the Irregular-moon system of Saturn, Figure 2B of all Irregular-moon systems of the giant planets (in two plots). Table 7A lists the orbit properties of 30 Saturnian Irregulars in one sheet (all 122 objects in .txt format →here).
At the end of the Cassini mission in Sep 2017, 38 Irregular moons of Saturn were on the records. In Oct 2019, orbits of twenty additional objects have been announced, provisionally designated as S/2004 S 20 to S/2004 S 39. [‘S/’ stands for ‘satellite’, ‘2004’ for the year of the oldest images where the object was detected, the second ‘S’ for ‘Saturn’, and the numbers ’20’, ’21’, ’22’, …, ’39’ are a continuous count.] In summer 2021, thirteen of these moons received permanent IAU designations (‘Saturn LIV’ to ‘Saturn LXVI’), and ten of them got names in August 2022. In fall 2021, orbit properties of newly discovered object S/2019 S 1 were provided. In early May 2023, sixty-two more moons have been announced, another one late in May. These detections increase the total count of Saturnian Irregular moons to 122 objects. It is for sure that numerous smaller objects exist, the smaller the more. An estimate from 2021 assumes that at least ∼100, maybe up to ∼150 objects larger than ∼3 kilometers populate the Saturnian Irregular moon system. Interstingly, this number is about three times larger than in the Jovian Irregular-moon system where approximately 30 to 40 objects down to a size of ∼3 km exist.
→ Table 7A (Orbital properties of 30 moons)
← table on basic properties of 122 Saturnian Irregular moons in text format
References (orbit properties): Denk+ (2018); Jacobson+ (2022); Ashton+ (2021); Nesvorný+ (2014); Bottke+ (2010); Nicholson+ (2008); Nesvorný+ (2007); Jewitt+ (2006); Jewitt and Haghighipour (2007); MPC Newsletter (2023); Sheppard (2006); Sheppard+ (2023)
(2A) a,e,i plot of Saturn’s Irregular moons
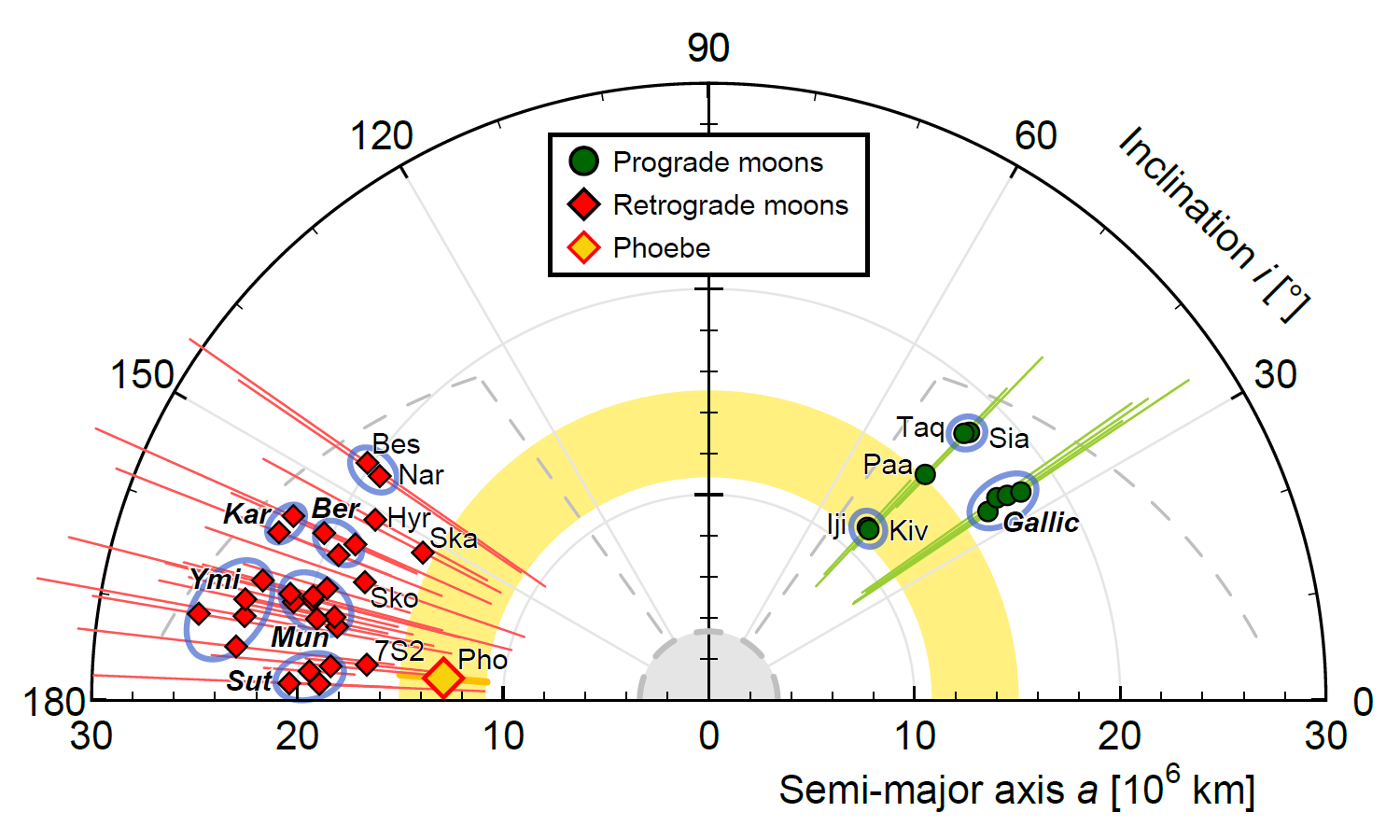
Polar plot of the a,i (semi-major axis, inclination) space for the 38 Irregular moons of Saturn known since 2007, adapted from Fig. 1 on page 412 in Denk et al. (2018). The thin bars are proxies for the eccentricities e, by showing periapsis and apoapsis distances of each object.
• The yellow band indicates the sphere of influence of Phoebe.
• The dashed lines show the inner boundary and apparent outer boundaries of the semi-major axes and inclinations for the Irregulars.
• Potential families or pairs are encircled by blue lines.
• Individual moons are labelled (by the first three letters of their names; see also Table 7A) except for members of possible families where only the name of the family is given (emphasized characters). These include:
Gallic — Alb, Beb, Err, Tar
Sut — Gre, 7S3, Sut, Thr
Mun — 4S13, Mun, Jar, 4S17, Hat, 4S12, Aeg, 4S7
Ber — 6S1, Ber, Far
Kar — Kar, 6S3
Ymi — Fen, Sur, Log, Ymi, For
(2B) a,i and P,i plots of the Irregular moons in the Solar System
 |
 |
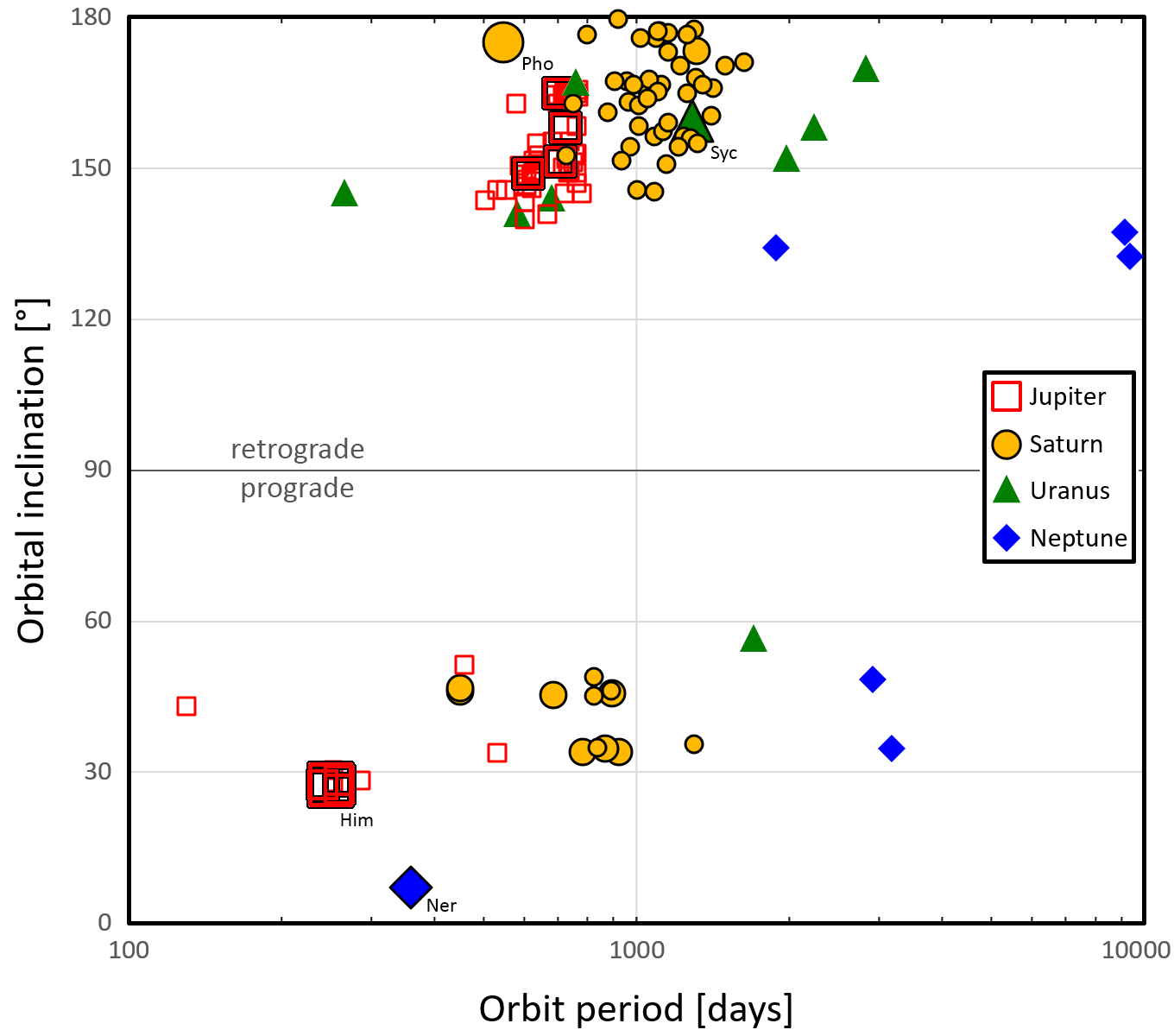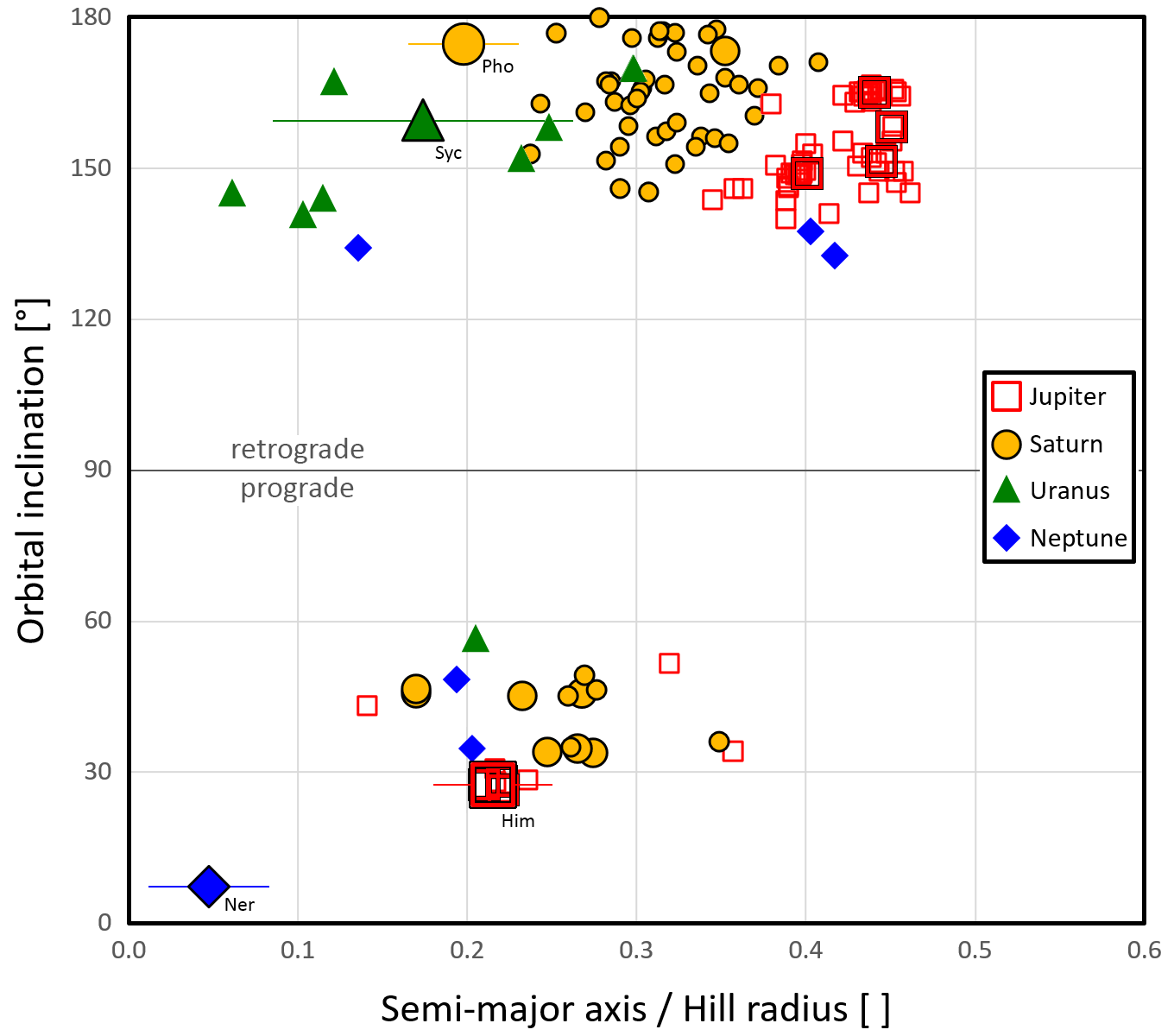
Plots of (Fig. left) the a,i (semi-major axis, inclination) and (Fig. right) P,i (orbital period, inclination) space for 144 Irregular moons of Jupiter (71 objects), Saturn (58), Uranus (9), and Neptune (6). Objects on retrograde orbits (i > 90°) are way more numerous than prograde Irregular moons. No moon at ∼60° < i < ∼130° was discovered so far. Except for Neptune’s dominating Nereid, there is also no Irregular moon known at i < 26°, and except for the Saturn system, no Irregular moon with i > 170° was found.
• The more recent findings since 2019 — 64 Saturnian (S/2004 S 40 to S 53, S/2005 S 4 to S 5, S/2006 S 9 to S 20, S/2007 S 5 to S 9, S/2019 S 1 to S 21, and S/2020 S 1 to S 10), 16 Jovian (S/2003 J 24, S/2011 J 3, S/2016 J 3 and J 4, S/2018 J 2 to J 4, S/2021 J 1 to S/2021 J 6, and S/2022 J 1 to J 3), 1 Uranian (S/2023 U 1) plus 2 Neptunian Irregulars (S/2002 N 5 and S/2021 N 1) — are not yet included in the plots. They increase the total known number of Irregular moons to 227, including 87 at Jupiter, 122 at Saturn, 10 at Uranus, and 8 at Neptune.
• The semi-major axes are given in units of planet Hill sphere radii (Jupiter: 53.1·106 km = 0.355 au = 743 RJ; Saturn: 65.5·106 km = 0.438 au = 1090 RS; Uranus: 70.1·106 km = 0.469 au = 2740 RU; Neptune: 116.1·106 km = 0.776 au = 4690 RN). Despite the smaller masses of Uranus and Neptune compared to Jupiter and Saturn, their Hill spheres are larger because they are further away from the Sun.
• Each system is dominated by one object which posesses more than three-quarters of the mass of the respective Irregular moon system. These are: Himalia (at Jupiter; ∼75% of the mass); Phoebe (Saturn; ∼98%); Sycorax (Uranus; ∼90%); Nereid (Neptune; ∼98%). They are marked by large symbols, and are labelled. Furthermore, their varying ranges to the planet (periapsis to apoapsis distances) are indicated by thin horizontal bars in the figure to the left.
• Nereid (diameter ∼340 km) is the largest of the outer moons in the Solar System and contains about two-thirds of the whole mass. With ∼17% of the mass, Phoebe (∼213 km) is second, followed by Sycorax (∼160 km; ∼7%) and Himalia (∼120×150 km; ∼5%). All other outer moons share the remaining ∼4% of the total mass.
• For the 34 Irregulars with presumed diameters larger than ∼10 km, a larger symbol size is chosen than for the smaller objects. For Uranus and Neptune, no Irregular moon smaller than ∼8 km is known yet, although such objects certainly exist — they were simply too dark for past search campaigns (with R-magnitude limits of 26.1 mag and 25.8 mag, respectively).
• Dynamical grouping is especially obvious for the Jovian moons, indicating that many of them are remnants of larger objects which have been destroyed through collisions. It appears likely that this happened also in the other systems. For Saturn, several such “dynamical families” have been suggested although the evidence from today’s orbital elements appears rather weak. For Uranus and Neptune, only little can be said because small moons have not been discovered yet. See also sheet (6).
• No known outer moon has a semi-major axis >0.47 Hill radii. (A formerly suspicious object with the temporary designation S/2003 J 2 was unmasked being an ordinary member of the Ananke family.)
• The outer moon with the shortest orbit period is Jupiter’s Themisto (sidereal period P = 130 d). The Irregular moon closest to Uranus is named Francisco; its orbit period is ~270 d. Nereid (closest to Neptune) needs almost exactly one year (P = 359 d) for one revolution around the planet. The Irregular satellites closest to Saturn is S/2019 S 1 (P = 446 d).
• Neptune’s outermost satellites Psamathe (P ∼ 9150 d), Neso (P ∼ 9800 d), and S/2021 N 1 (P ∼ 10000 d) require more than 25 years to orbit once around Neptune. One may thus expect that they experienced much less collisions with other Irregular moons than the other objects with much shorter orbit periods.
• Neptune’s largest moon Triton is also considered “irregular”; but it is not included in the plot because it is not just very different in size, distance to the planet, and “everything” to the outer Irregular moons, but also because its origin, capture, and dynamical-evolution stories are likely very different as well. Furthermore, the precession of Triton’s orbital plane is dominated by the planet’s oblateness and not by the Sun. Iapetus (P = 80 d) might be regarded as an irregular satellite too, but even if so, its not really understood story is also another one.
(3) Cassini observations
With the Cassini-ISS camera, 25 Irregular moons of Saturn have been observed. Because the moons (except Phoebe) are quite small and were far away from the spacecraft (> 10 million km for most of the time), they appeared only as light dots (formally) smaller than a pixel on the CCDs of the cameras. The goal was thus to obtain lightcurves through disk‐integrated photometric studies to determine basic physical quantities like rotation periods, pole‐axis orientations, shapes, sizes, phase curves, and colors. During the Cassini mission, my responsibility was the observation planning (overall strategy as well as all practical details). An overview of this task is given on this website and is quite nicely illustrated by the cartoon to the right.
For our Irregular-moon observations, we used the Narrow-Angle Camera (NAC) of the Imaging Science Subsystem (ISS) of Cassini (Fig. right). The NAC was a spacecraft‐fixed f/10.5 Ritchey‐Chrétien reflector telescope with a focal length of 2 m and an aperture of 7.5 inches (~19 cm). The size of the CCD detector was 1024×1024 pixels, the field‐of‐view was 0.35° or 21 arcminutes, and color information was obtained through color filters. During lightcurve observations, we usually operated the NAC with the broadband “clear” filter in “summation mode” (2×2 pixel binning on the CCD, resulting in 512×512‐pixel images; pixel size 2.5 arcseconds). A typical exposure time was 220 seconds. The total number of images targeting Irregular moons throughout the Cassini mission is ~38,000.
Correct pointing was an issue for 21 of the 38 objects known at this time. For 12 of them, the predicted ephemeris accuracy was deemed too low. For the other nine, the hit probability was moderate, and we succeeded for eight of them (only Surtur escaped us). This sums up to the total of 25 observed objects mentioned above.
The individual moon pages (sheet 1) provide high-level details of the observations and results.
Fig. 3A gives an example of Cassini-ISS images of an Irregular moon.
Fig. 3B shows exemplarily the orbits of five Irregulars as seen from the Cassini spacecraft, plus a “snapshot” of all Irregulars on a particular day in the “sky of Cassini”.
Fig. 3C offers a diagram showing the pointing accuracy of the Irregular-moon observations with Cassini ISS.
Sheet 3D provides a high-level planning overview (“SPASS”) of all Irregular-moon observations of Cassini.
The imaging observation planning site gives a general description of the Cassini planning procedure.
The only Irregular moon of Saturn where high-resolution images could be taken by Cassini is Phoebe. During approach to Saturn in June 2004, a targeted flyby at a minimum distance of 2071 km has been performed.
Outside the Saturn system, Cassini also observed Himalia, the largest Irregular moon of Jupiter, during the Jupiter flyby in December 2000. In the images, Himalia appears as a small disk ~4×6 pixels across.
Other spacecraft that observed Irregular moons during giant-planet flybys were New Horizons (Jupiter’s Himalia and Elara, both in Feb 2007) and Voyager 2 (Saturn’s Phoebe in Sep 1981; Neptune’s Nereid in Aug 1989).
References (Cassini observations): Denk and Mottola (2019; observations of Irregular moons with Cassini ISS); Knowles (2018; ISS data user’s guide); Porco+ (2004; general ISS description)
(3A) Example of Irregular-moon images from Cassini ISS
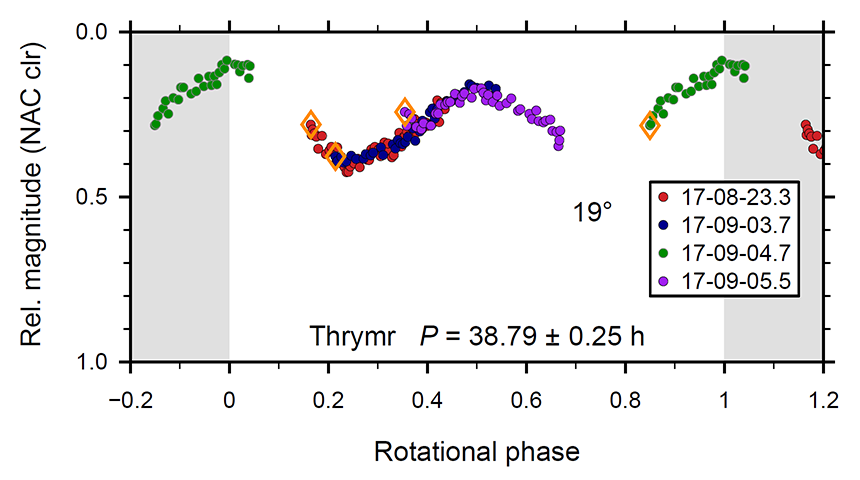
The last Cassini observations of an Irregular moon were performed on 23 Aug 2017 and from 03 to 06 Sep 2017 during four observations of object Thrymr. As an example for a calibrated data set, the images of these final Thrymr observations are provided as an animated gif. Thrymr is the jittering spot at the frame center.
Observation details (request name; start date; phase angle; observation duration; number of images used for lightcurve):
ISS_289OT_THRYLU013_PRIME — 23 Aug 2017 — 13° phase — 10.65 h — 57 images.
ISS_291OT_THRYTANJ016_PRIME — 03 Sep 2017 — 18° phase — 12.56 h — 46 images.
ISS_291OT_THRYTIM020_PRIME — 04 Sep 2017 — 19° phase — 7.44 h — 29 images.
ISS_291OT_THRYDARI022_PRIME — 05 Sep 2017 — 20° phase — 12.19 h — 43 images.
Notes:
• During calibration, the images were zoomed by a factor of 2 and cropped to 400×600 pixels.
• The still shows the very last image of an Irregular moon taken by Cassini.
• The lightcurve measured from these images is shown in the Fig. to the left.
(3B) Irregular moons in the sky of Cassini
 |
 |
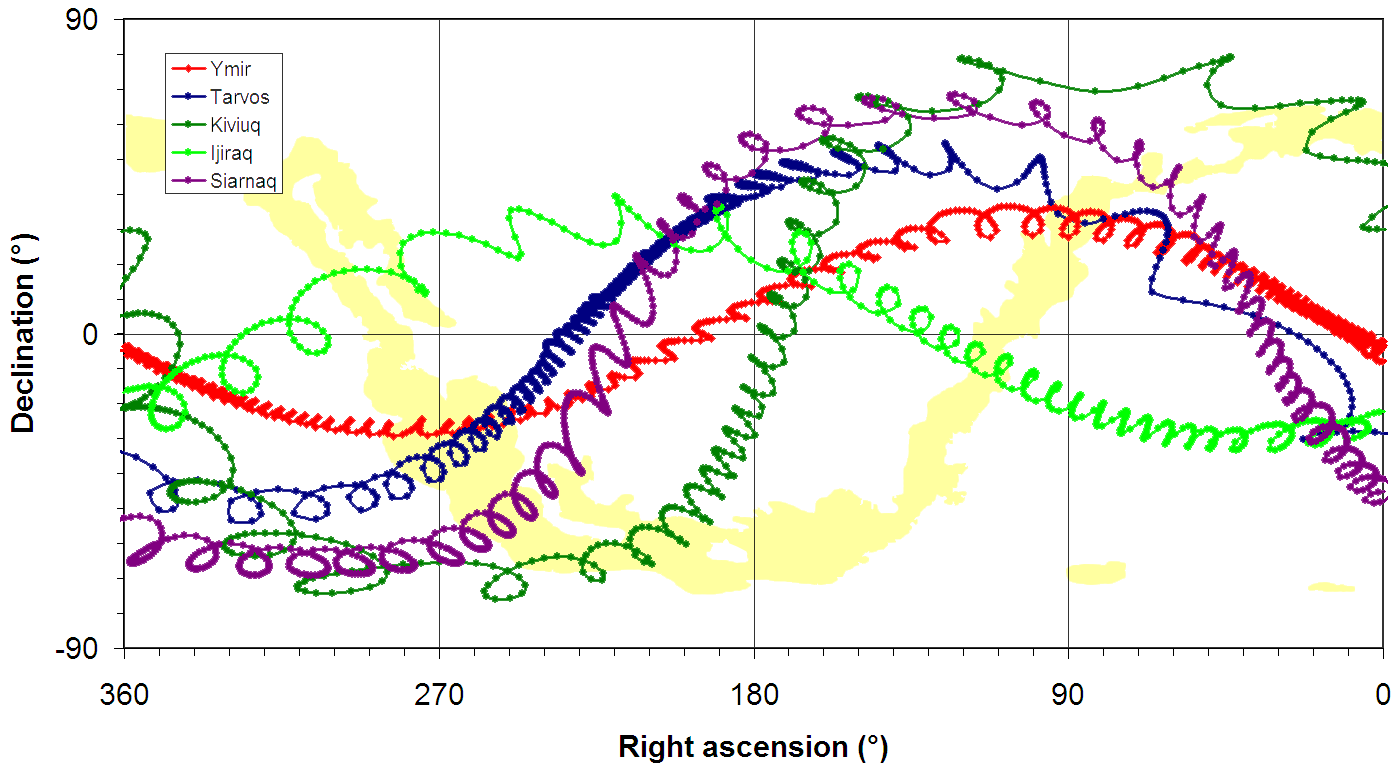
| Orbit paths of the five moons Ijiraq, Kiviuq, Siarnaq, Tarvos, and Ymir as seen from Cassini in the time frame 2010 to 2014. For each satellite, one orbit around Saturn is shown.
• Cylindrical projection; in geocentric coordinates. |
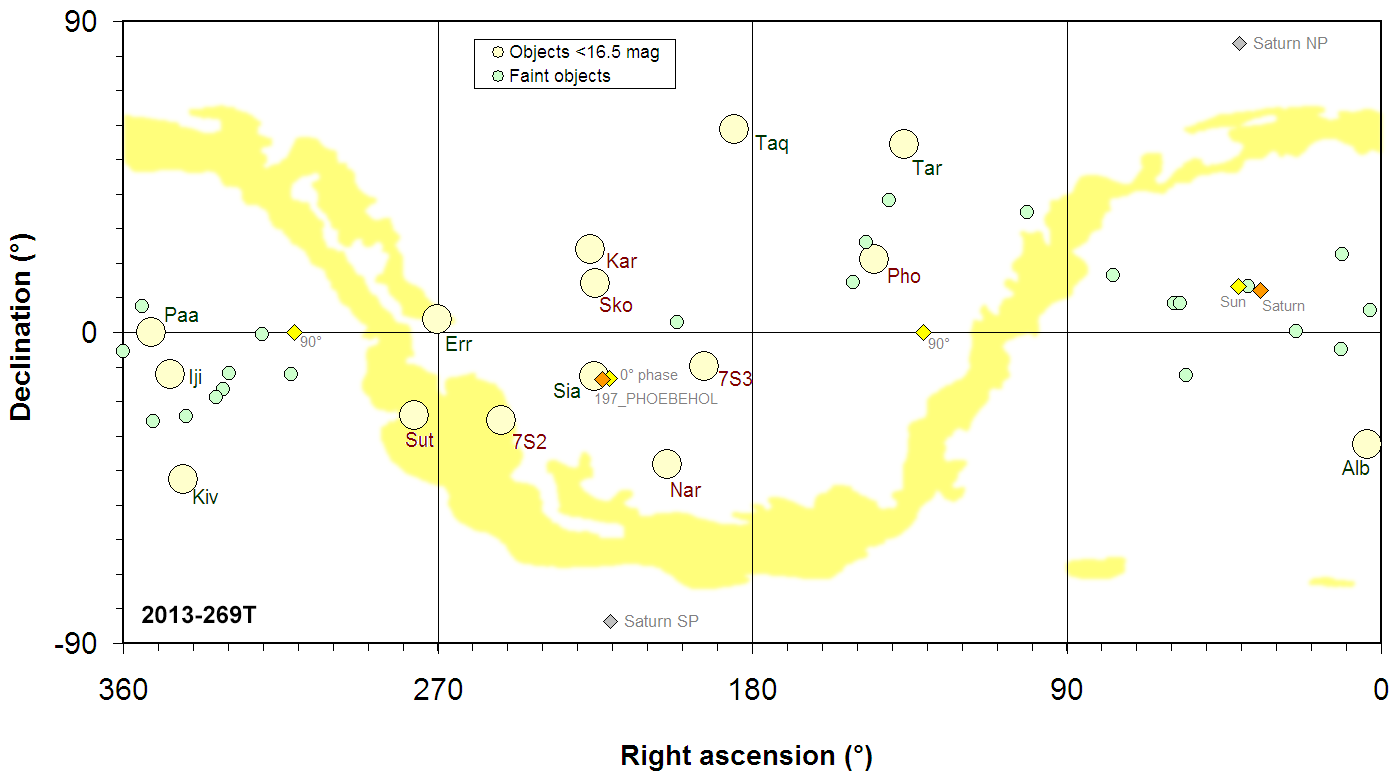
Snapshot of “Cassini’s sky” from 26 Sep 2013, showing the locations of the 38 Irregular moons known at this time. Objects with visual magnitude <16.5 are labelled.
• These would have been observable in principle by the NAC at this epoch. |
(3C) Cassini imaging pointing accuracy
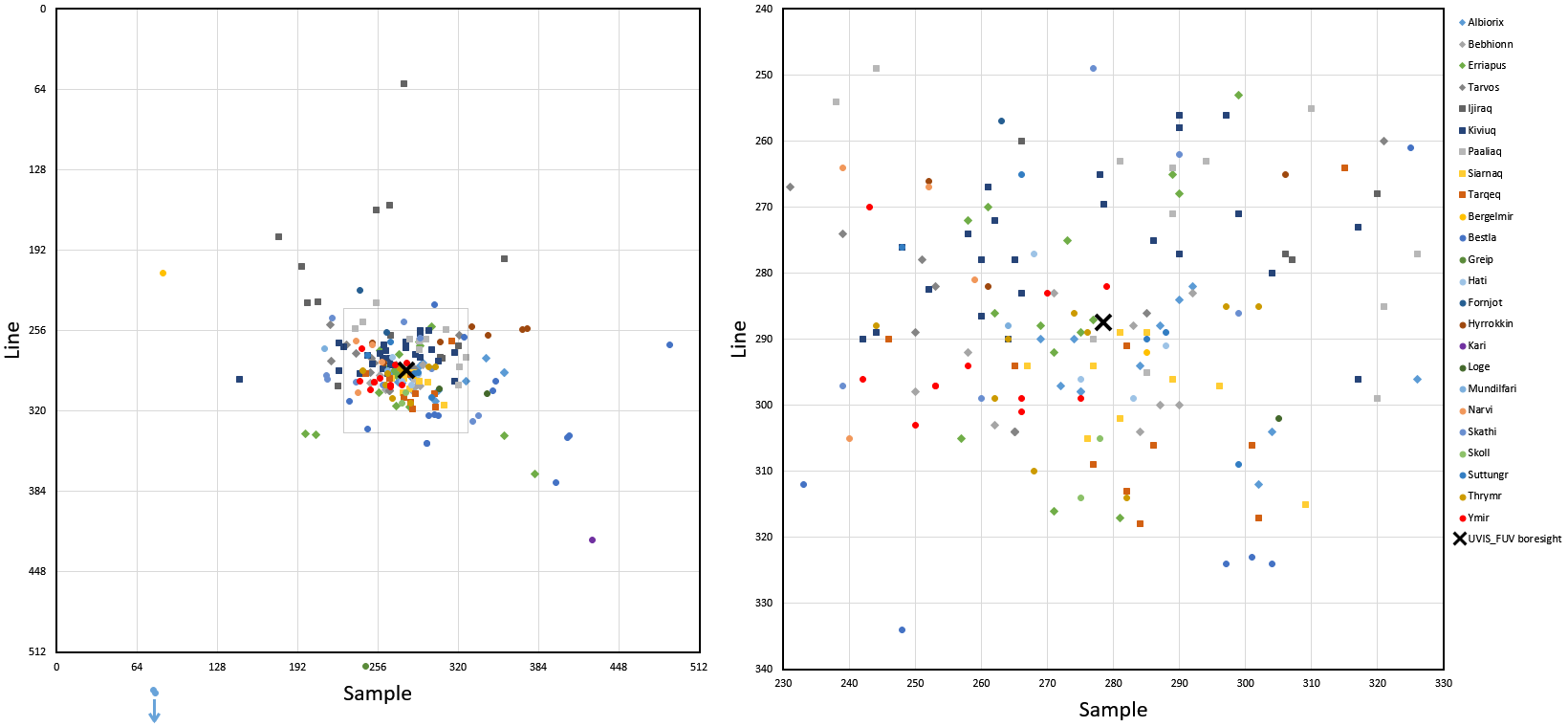
Irregular-moon pointings with the Cassini ISS-NAC (in summation mode).
Left: Complete field-of-view (512×512 pixels). Right: Enlarged cutaway view.
Notes:
• Pointing was never perfect because of imperfect object ephemeris and (to a small degree) of pointing limitations of the spacecraft at the “few-pixels level”. Otherwise, all dots in the diagrams would have landed on the black cross (boresight of the UVIS instrument).
• Two observations of Hati and one of Greip felt outside the NAC field-of-view, but trapped the object because a 1×2 mosaic was performed.
• For some observations, a horizontal offset to the left was commanded. For the diagram, these pointings are shifted back as if no offset were commanded.
(3D) High-level planning overview of all Irregular-moon observations
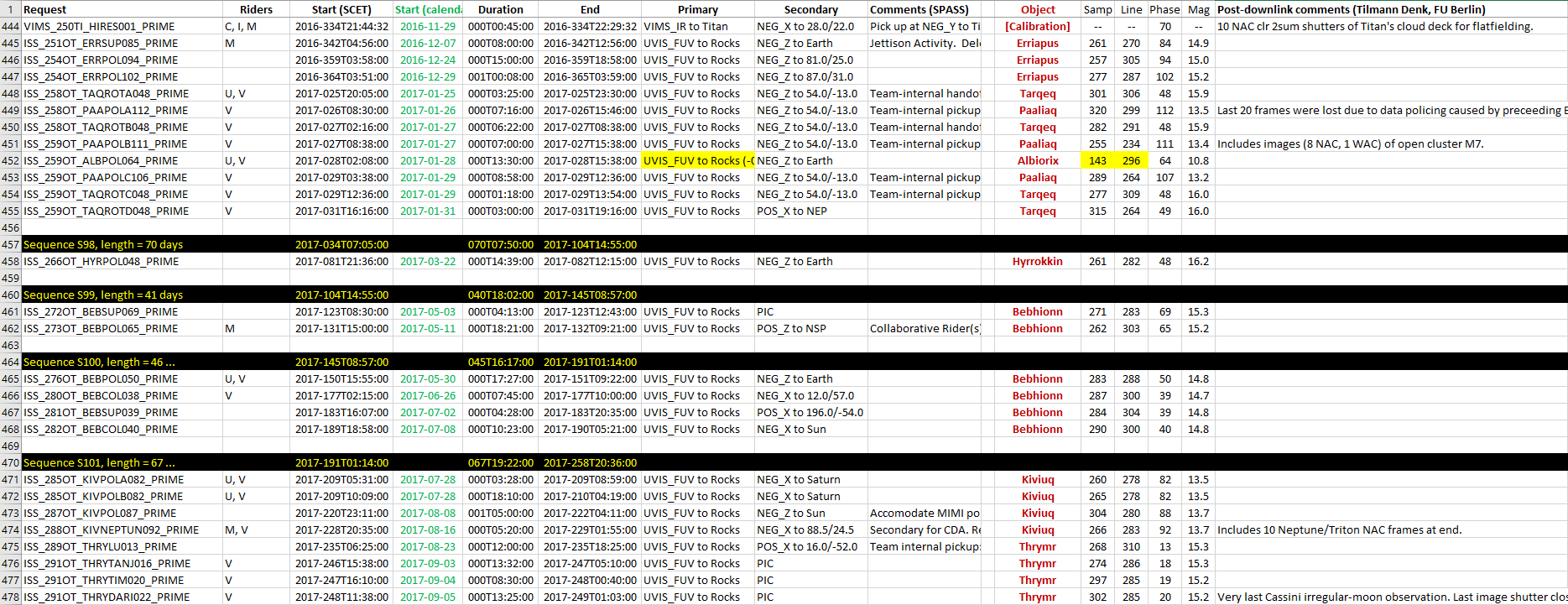
Excel file — pdf file — text file
This spreadsheet summarizes the Irregular-moon planning observations as they appeared in the “SPASSes” during the mission. In addition, it includes data notes like object positions on the CCD of the Cassini camera, or observation phase angles.
Notes:
• “SPASS” = Spacecraft attitude spreadsheet. It lists the spacecraft attitude of each observation request. The SPASS was a key product for the planning of the Cassini activities.
• In the pdf and text file (ASCII) versions, some information is lost compared to the Excel file.
• This table (somehow) summarizes all Cassini observations of Irregular moons. I compiled it from many sources over the years while Cassini was still active. Especially when working with the data, you might find it useful. I hope that it contains only minor errors — ideally none —, and that it is complete with respect to the performed observations.
• For this table, information from the Cassini Project’s SPASSes was copied into columns A to I. In addition, calendar dates were included in column D, and object names, approximate sample/line positions in the images (= x,y in Photshop) (the origin is at upper left), observation phase angles, calculated magnitudes (calculated for planning purposes), plus additional potentially useful remarks are added in columns K to P. See also notes at start and end in the table.
(4) Rotation periods and sizes
Rotation periods could be determined from lightcurves for 25 Irregular moons of Saturn. Twenty of them are secure, an ambiguity remained for three, and two are tentative. The values range from 5.42 hours (Hati) to 76.13 hours (Tarqeq). The average spin rate for 22 Irregular moons of Saturn (all except Phoebe, Loge, Fornjot) is 2.10 d−1, the corresponding average period is 11.4 h. Remarkably, it appears that there exist dependencies between spin rates, object sizes, distances to Saturn, and orbit directions. The retrogradely orbiting Irregular moons of Saturn are on average rather small, far away from the planet, on less tilted orbits, and have comparably fast rotations, while the prograde satellites are mostly large, orbit closer to Saturn, at higher inclinations, and rotate more slowly.
In comparison to other minor bodies in the solar system, the mean of the spin rates of the Saturnian Irregulars is significantly lower than of the main-belt asteroids (for the same size range), but similar to Hilda and Jupiter Trojan asteroids (see Fig. 4B). The absence of very fast rotators among the Irregulars indicates that these objects might have rather low densities, possibly as low as comets.
The sizes of Saturn’s known Irregular moons (except Phoebe) range from ∼40 km (Siarnaq) to ∼3 km (approximate detection limit of the search campaign from 2004 to 2007). Since no disk-resolved observations exist so far, they are estimated through the absolute magnitudes (determined from ground-based telescopes) and albedo estimates. For the diameter calculation, see note #7 of the tables in sheet (7).
→ Table 7B (Physical properties)
← table on basic properties of 59 Saturnian Irregular moons in text format
References (periods and sizes): Gomes-Júnior+ 2020; Denk and Mottola (2019); Denk+ (2018); Bauer+ (2004)
(4A) Lightcurves of Irregular moons
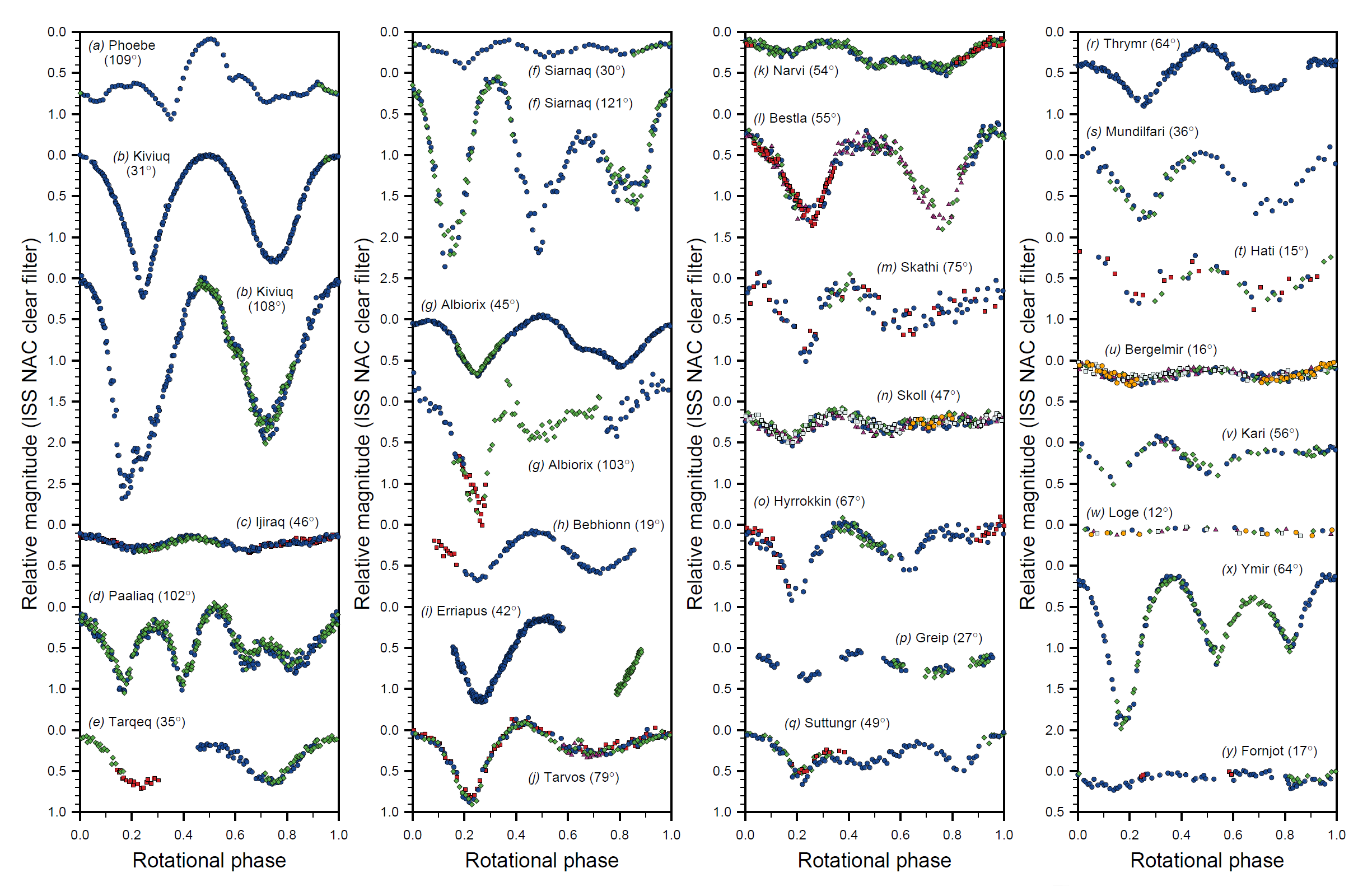
Lightcurves of 25 Irregular moons of Saturn, taken with Cassini ISS NAC at the annotated phase angles; adapted from Fig. 2 on page 418 in Denk et al. (2018).
Different symbols indicate different rotational cycles from the same observation or from another observation close in time. See the individual-moon websites for observation details.
(4B) Object diameters versus spin rates for various groups of solar system objects
Shown are objects with sizes between 4 km and 45 km and with spin rates below 10 d−1. Adapted from Fig. 6 on page 424 in Denk et al. (2018).
NEA/MC — Near Earth Asteroids / “Mars Crossers”
MBA — Main Belt Asteroids
Hilda — “Hilda asteroids” are in 3:2 resonance with Jupiter’s orbit about the Sun
Jupiter Trojans — are in 1:1 resonance with Jupiter near the L4 and L5 Lagrange points
Centaurs — minor bodies residing between Jupiter and Neptune
TNO — Trans Neptunian Objects
• The average rotational periods for this size range are as follows [in brackets for sizes 10 to 45 km]: NEAs/MCs: 5.4 h [6.1 h]; MBAs: 6.4 h [7.0 h]; Hildas: 10.2 h [10.2 h]; Jupiter Trojans: N/A [11.3 h]; Saturn Irregulars: 11.4 h [14.2 h]; Centaurs and TNOs: ~13 h.
• The plotted data, except for the Saturnian Irregular moons, are from the Asteroid Lightcurve Database (LCDB) (Warner et al. 2009, accessed on September 5, 2016).
(5) Pole, shape, seasons
Depending on viewing directions and data quality, the lightcurves of the moons might be useful to compile shape models, sidereal periods, and pole directions (coordinates in the sky to which the rotational axis of an object points).
The preliminary shape model of Siarnaq from seven observations indicates that this moon resembles a triangular prism (in the convex model). The pole axis (north pole) points toward ecliptic longitude and latitude λ / β = 98° / −23° ± 15°. This rather low latitude indicates that Siarnaq experiences extreme seasons, somewhat reminiscent of the regular satellites of Uranus. During summer solstice, the Sun might reach the zenith at a surface latitude of 60° to 70° on one hemisphere, while the other remains in a many-years lasting darkness. The most recent summer solstice on the northern hemisphere occured in mid-2018.
The shape model of Ymir also revealed a triangular equatorial cross-section very similar to Siarnaq. The pole-axis of Ymir points close to the south-ecliptic pole, indicating a retrograde spin and no noticeable seasonal variations on the surface. See the Ymir page for more details.
References (pole/shape): Denk+ (2018); Giese+ (2006); Kaasalainen+ (2001)
(5A) Example: Shape model of Siarnaq
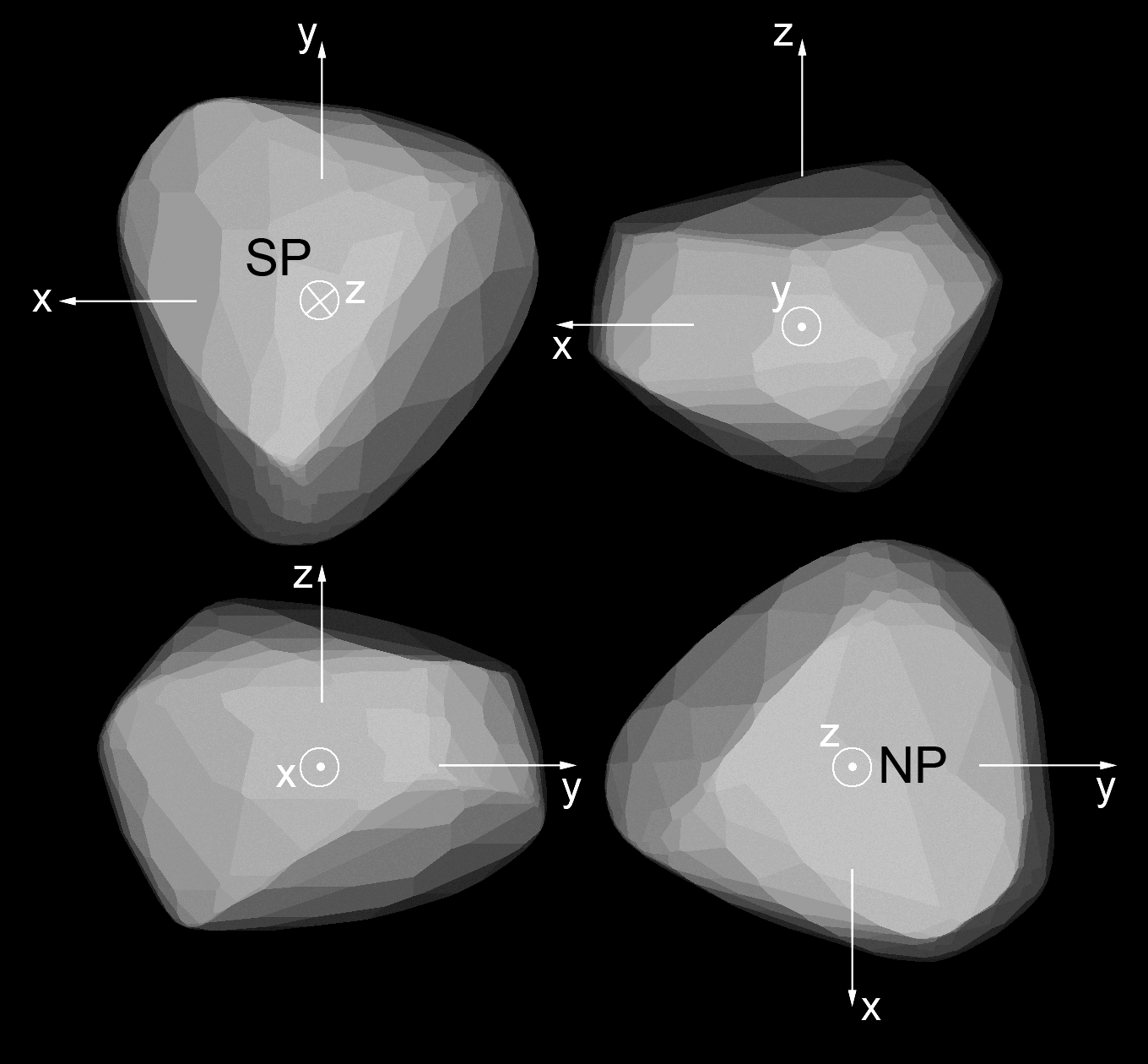
Preliminary shape model of Siarnaq. The z-axis is the rotation axis.
Important: The used technique to determine convex-shape models cannot reproduce concavities like craters or other constrictions.
(6) Origin of the Irregular moons
The Irregular satellites of the giant planets have defied conventional origin models for some time. The shapes of their cumulative size-frequency distributions are unlike any small body population seen anywhere in the solar system. Outside the largest objects (Himalia at Jupiter, Phoebe at Saturn, Sycorax at Uranus, Nereid at Neptune), they tend to have very little mass. The colors are consistent with dark C-, P-, and D-type asteroids, which are common among the Hilda and Trojan asteroid populations as well as in the outer asteroid belt, but are also a good match to the observed dormant comets.
Several capture scenarios have been described in the literature. Most promising, three-body capture using three-body exchange reactions between a binary planetesimal and the primary planet has been considered.
An important aspect of Irregular satellites is that they were captured into a relatively tiny region of space with short orbital periods around Saturn. This makes high-velocity collisions between Irregular satellites unavoidable. Moreover, collision probabilities between typical Irregular satellites are four orders of magnitude (factor of ∼10000) higher than those found among main-belt asteroids. A prediction is that the Irregular-moon populations of the giant planets have lost ~99% of their mass via impacts, making them the most collisionally evolved populations in the solar system. Among Saturn’s Irregulars, Phoebe is presumably the only primordial object, while all others should be remnants of collisions.
References (origin): Denk+ (2018); Ashton+ (2021); Nesvorný+ (2014); Bottke+ (2010); Nicholson+ (2008); Grav and Bauer (2007); Jewitt and Haghighipour (2007); Nesvorný+ (2007); Sheppard (2006); Sheppard+ (2023)
(7) Overview tables
The tables provide fundamental numbers of the 30 Irregular moons that were known and had names during the Cassini mission (i.e., before 2017).
Table 7A contains orbital properties, Table 7B physical properties.
Notes for both tables are given below Table 7B.
← Table on basic properties of 122 Saturnian Irregular moons in text format (updated 04 Jul 2023).
More numbers for all moons are provided on the individual moon websites (sheet 1).
References (overview tables): Denk and Mottola (2019); Denk+ (2018); Jacobson+ (2022)
(7A) Orbital properties of Saturn’s Irregular moons
| SPICE ID (1) | Moon | Year of discovery (2) | Group member (3) | Semi-major axis [106 km] (4) |
Orbital period [a] (4) |
Eccentricity [ ] (4) |
Inclination [deg] (4) |
On-sky uncertainty [ ” ] (5) |
Moon (abbrev.) (11) |
| 609 | Phoebe | 1899 | retro | 12.929 | 1.507 | 0.16 | 175.2 | <0.01 | Pho |
| 619 | Ymir | 2000 | retro | 22.957 | 3.601 | 0.34 | 173.1 | 0.04 | Ymi |
| 620 | Paaliaq | 2000 | Inuit | 14.997 | 1.881 | 0.38 | 47.1 | 0.02 | Paa |
| 621 | Tarvos | 2000 | Gallic | 18.215 | 2.536 | 0.53 | 38.6 | 0.24 | Tar |
| 622 | Ijiraq | 2000 | Inuit | 11.345 | 1.236 | 0.35 | 49.2 | 0.08 | Iji |
| 623 | Suttungr | 2000 | retro | 19.392 | 2.784 | 0.12 | 175.0 | 0.20 | Sut |
| 624 | Kiviuq | 2000 | Inuit | 11.307 | 1.230 | 0.18 | 48.9 | 0.01 | Kiv |
| 625 | Mundilfari | 2000 | retro | 18.590 | 2.609 | 0.21 | 168.4 | 0.28 | Mun |
| 626 | Albiorix | 2000 | Gallic | 16.329 | 2.145 | 0.47 | 38.9 | 0.02 | Alb |
| 627 | Skathi | 2000 | retro | 15.575 | 1.993 | 0.27 | 149.7 | 0.03 | Ska |
| SPICE ID (1) | Moon | Year of discovery (2) | Group member (3) | Semi-major axis [106 km] (4) |
Orbital period [a] (4) |
Eccentricity [ ] (4) |
Inclination [deg] (4) |
On-sky uncertainty [ ” ] (5) |
Moon (abbrev.) (11) |
| 628 | Erriapus | 2000 | Gallic | 17.507 | 2.385 | 0.46 | 38.7 | 0.02 | Err |
| 629 | Siarnaq | 2000 | Inuit | 17.881 | 2.453 | 0.31 | 48.2 | 0.03 | Sia |
| 630 | Thrymr | 2000 | retro | 20.327 | 2.989 | 0.47 | 174.8 | 0.02 | Thr |
| 631 | Narvi | 2003 | retro | 19.287 | 2.748 | 0.45 | 143.7 | 0.44 | Nar |
| 636 | Aegir | 2005 | retro | 20.665 | 3.065 | 0.26 | 166.9 | 0.58 | Aeg |
| 637 | Bebhionn | 2005 | Gallic | 17.029 | 2.286 | 0.48 | 37.4 | 0.01 | Beb |
| 638 | Bergelmir | 2005 | retro | 19.269 | 2.753 | 0.14 | 158.7 | 1.04 | Ber |
| 639 | Bestla | 2005 | retro | 20.338 | 2.977 | 0.46 | 136.3 | 0.09 | Bes |
| 640 | Farbauti | 2005 | retro | 20.293 | 2.977 | 0.25 | 157.7 | 2.55 | Far |
| 641 | Fenrir | 2005 | retro | 22.332 | 3.450 | 0.14 | 164.3 | 1.04 | Fen |
| SPICE ID (1) | Moon | Year of discovery (2) | Group member (3) | Semi-major axis [106 km] (4) |
Orbital period [a] (4) |
Eccentricity [ ] (4) |
Inclination [deg] (4) |
On-sky uncertainty [ ” ] (5) |
Moon (abbrev.) (11) |
| 642 | Fornjot | 2005 | retro | 24.937 | 4.091 | 0.21 | 169.5 | 0.33 | For |
| 643 | Hati | 2005 | retro | 19.697 | 2.848 | 0.38 | 164.1 | 0.15 | Hat |
| 644 | Hyrrokkin | 2006 | retro | 18.343 | 2.551 | 0.33 | 150.3 | 1.20 | Hyr |
| 645 | Kari | 2006 | retro | 22.030 | 3.370 | 0.48 | 153.0 | 0.39 | Kar |
| 646 | Loge | 2006 | retro | 22.918 | 3.592 | 0.19 | 166.9 | 0.79 | Log |
| 647 | Skoll | 2006 | retro | 17.626 | 2.405 | 0.47 | 158.4 | 0.60 | Sko |
| 648 | Surtur | 2006 | retro | 22.754 | 3.550 | 0.45 | 168.3 | 9.40 | Sur |
| 650 | Jarnsaxa | 2006 | retro | 19.280 | 2.757 | 0.22 | 163.0 | 47.46 | Jar |
| 651 | Greip | 2006 | retro | 18.380 | 2.565 | 0.32 | 173.4 | 2.05 | Gre |
| 652 | Tarqeq | 2007 | Inuit | 17.748 | 2.423 | 0.12 | 49.7 | 0.08 | Taq |
(7B) Physical properties of Saturn’s Irregular moons
| SPICE ID (1) | Moon | Year of discovery (2) | Absolute magnitude HV [mag] (6) |
Range for mean diameter [km] (7) |
Lightcurve amplitude [mag] (8) |
Rotation period [h] (9) |
Color B−R [mag] (10) |
Moon (abbrev.) (11) |
| 609 | Phoebe | 1899 | 6.6 | 212 … 214 | 0.34 (29°) | 9.27365 | 0.98‡ ; 0.91¶ | Pho |
| 619 | Ymir | 2000 | 12.3 | 16 … 25 | 0.63 (29°) | 11.9222 | 1.22‡ | Ymi |
| 620 | Paaliaq | 2000 | 11.7 | 21 … 33 | 0.10 (21°) | 18.79 | 1.26‡ | Paa |
| 621 | Tarvos | 2000 | 12.9 | 12 … 19 | 0.18 (38°) | 10.691 | 1.21‡ ; 1.13¶ | Tar |
| 622 | Ijiraq | 2000 | 13.2 | 11 … 16 | 0.20 (47°) | 13.03 | 1.63‡ ; 1.40¶ | Iji |
| 623 | Suttungr | 2000 | 14.5 | 6 … 9 | 0.25 (12°) | 7.67 | 1.12‡ | Sut |
| 624 | Kiviuq | 2000 | 12.6 | 14 … 22 | 1.71 (31°) | 21.97 | 1.38‡ | Kiv |
| 625 | Mundilfari | 2000 | 14.5 | 6 … 9 | 0.78 (36°) | 6.74 | 0.99‡ | Mun |
| 626 | Albiorix | 2000 | 11.1 | 23 … 34 | 0.72 (45°) | 13.33 | 1.35‡ ; 1.29¶ | Alb |
| 627 | Skathi | 2000 | 14.3 | 6 … 10 | 0.38 (15°) | 11.10 | 1.09‡ | Ska |
| SPICE ID (1) | Moon | Year of discovery (2) | Absolute magnitude HV [mag] (6) |
Range for mean diameter [km] (7) |
Lightcurve amplitude [mag] (8) |
Rotation period [h] (9) |
Color B−R [mag] (10) |
Moon (abbrev.) (11) |
| 628 | Erriapus | 2000 | 13.7 | 8 … 13 | 0.98 (42°) | 28.15 | 1.11‡ ; 1.19¶ | Err |
| 629 | Siarnaq | 2000 | 10.6 | 33 … 45 | 0.33 (30°) | 10.1879 | 1.36‡ | Sia |
| 630 | Thrymr | 2000 | 14.3 | 6 … 10 | 0.30 (19°) | 38.79 (?) | 1.00‡ | Thr |
| 631 | Narvi | 2003 | 14.4 | 6 … 9 | 0.37 (54°) | 10.21 | 1.29¶ | Nar |
| 636 | Aegir | 2005 | 15.5 | 4 … 6 | — | ? | 1.30¶ | Aeg |
| 637 | Bebhionn | 2005 | 15.0 | 5 … 7 | 0.58 (19°) | 16.33 | 1.12¶ | Beb |
| 638 | Bergelmir | 2005 | 15.2 | 4 … 7 | 0.20 (16°) | 8.13 | 1.10¶ | Ber |
| 639 | Bestla | 2005 | 14.6 | 6 … 9 | 0.90 (41°) | 14.624 | 1.32¶ | Bes |
| 640 | Farbauti | 2005 | 15.7 | 3 … 5 | — | ? | ? | Far |
| 641 | Fenrir | 2005 | 15.9 | 3 … 5 | — | ? | ? | Fen |
| SPICE ID (1) | Moon | Year of discovery (2) | Absolute magnitude HV [mag] (6) |
Range for mean diameter [km] (7) |
Lightcurve amplitude [mag] (8) |
Rotation period [h] (9) |
Color B−R [mag] (10) |
Moon (abbrev.) (11) |
| 642 | Fornjot | 2005 | 14.9 | 5 … 7 | 0.18 (17°) | 7 or 9.5 ? | 1.40¶ | For |
| 643 | Hati | 2005 | 15.3 | 4 … 6 | 0.55 (15°) | 5.42 | ? | Hat |
| 644 | Hyrrokkin | 2006 | 14.3 | 6 … 10 | 0.41 (20°) | 12.76 | 1.23¶ | Hyr |
| 645 | Kari | 2006 | 14.8 | 5 … 8 | 0.50 (56°) | 7.70 | ? | Kar |
| 646 | Loge | 2006 | 15.3 | 4 … 6 | 0.07 (12°) | 6.9 ? | ? | Log |
| 647 | Skoll | 2006 | 15.4 | 4 … 6 | 0.35 (47°) | 7.26 (?) | ? | Sko |
| 648 | Surtur | 2006 | 15.8 | 3 … 5 | — | ? | ? | Sur |
| 650 | Jarnsaxa | 2006 | 15.6 | 3 … 5 | — | ? | ? | Jar |
| 651 | Greip | 2006 | 15.4 | 4 … 6 | 0.32 (27°) | 12.75 (?) | ? | Gre |
| 652 | Tarqeq | 2007 | 14.8 | 5 … 8 | 0.60 (35°) | 76.13 | 1.37¶ | Taq |
Table notes:
[Back to Table 7A (orbital properties); Table 7B (physical properties)]
(1)…SPICE is a commonly-used information system of NASA’s Navigation and Ancillary Information Facility (NAIF). It assists engineers in modeling, planning, and executing planetary-exploration missions, and supports observation interpretation for scientists. Each planet and moon obtained a unique SPICE number. The SPICE IDs of Saturn’s Irregular moons are defined in this tpc-kernel.
(2)…Year of discovery announcement.
(3)…A coarse subdivision of the Irregular moons into three groups is dynamically justified. The objects in the prograde “Gallic group” have an inclination close to 38°, in the prograde “Inuit group” close to 47°. All other Irregulars orbit Saturn at retrograde paths, with inclinations ranging from ∼130° to almost 180°.
(4)…Mean orbital elements (the elements of a precessing ellipse which has been fit to the numerically integrated orbit); from JPL’s Solar-System dynamics website. [a] = years; [deg] = degrees.
(5)…Data from Table 5 in Jacobson et al. (2022); [ ” ] = arcseconds. The on-sky uncertainty is the statistical value for the deviation of the object’s location compared to the calculated position as seen from Earth for the epoch three orbital periods beyond January 2022. According to Jacobson et al. (2022), approximately four moons with values >60″ are in danger of getting lost, or have been effectively lost. Since these have not been named yet, they are not listed here. (These are S/2004 S 12 (lost), S/2004 S 36 (345″), S/2004 S 37 (187″), and S/2007 S 3 (lost).) In the meantime (early 2023), these moons have been recovered and none from the Jacobson et al. (2022) paper is in danger of getting lost anymore.
(6)…The visual absolute magnitude HV is the visual magnitude (brightness) of an object if located 1 au away from the Sun and observed at 0° phase angle (i.e., the observer virtually sits at the center of the Sun in this definition). Smaller numbers indicate brighter objects. The magnitude scale is logarithmic, with an object of 6th mag being 100× darker than a 1st mag object. For this table, data from MPEC were used for the absolute magnitudes (as of July 2017). Numbers from other sources may vary by several tenths of magnitudes (e.g., compare HV values from MPEC with a NASA Fact Sheet, JPL’s ssd page, or S. Sheppard’s page).
(7)…Calculated from absolute magnitude HV ± 0.01 and assumed albedo A = 0.06±0.02 through $D=1 \text{ au}\cdot \frac{2}{\sqrt{A}}\cdot 10^{−0.2·(H−M_☉)}$; with the solar apparent V magnitude M☉ = −26.71 ± 0.02 mag (Pecaut and Mamajek 2013) and the Astronomical Unit 1 au = 149 597 870.7 km (see also IAU Resolution B2). Note that the uncertainties for A and HV may be even larger (see note #6), and thus may be the ranges for the mean sizes. Phoebe’s value is from Thomas et al. (2018). The value ranges for Siarnaq and Albiorix are from Grav et al. (2015).
(8)…Maximum lightcurve amplitude from Cassini observations; no phase-angle corrections.
(9)…Highlighted fields indicate entries from our Cassini work (Denk et al. 2018). A question mark in brackets indicates a possible ambiguity of the period, a question mark without brackets that the period is tentative or unknown. The Phoebe value is from Gomes-Júnior et al. (2020).
(10)…From Grav and Bauer (2007) (marked by ‡) and Graykowski and Jewitt (2018) (marked by ¶). Given is the B−R color index, with mean wavelengths 445 nm and 658 nm for B and R filters, respectively. B−R of the Sun is 1.01 (Ramírez et al. 2012). A larger B−R index indicates a positive spectral slope (“reddish” object), while a B−R < 1 indicates a negative spectral slope (“bluish” object). The reason for different values of the five objects measured by both astronomer groups is likely mainly due to a different treatment of the phase function, see discussion in the Graykowski and Jewitt paper. So far, I do not think that there are true color variegations on the surfaces of the Irregulars except Phoebe, but this cannot be ruled out or confirmed so far with the published data.
(11)…These abbreviations are my own and not official. I used them as object identifiers for the Cassini observation planning (esp. in the request names) and also in figures in publications.
(8) Methods
The content for this sheet will be added at a later date. In the meantime, feel free to check the references: Mottola et al. (1995) for data measuring and period determination, Kaasalainen et al. (2001) and Mottola et al. (2023) for the lightcurve inversion method to determine shape models, West et al. (2010) for Cassini ISS data calibration, Denk and Mottola (2019) for Irregular-moon data calibration, processing, and measuring, or Knowles (2018) for general ISS data usage guidance.
References (methods): Mottola+ (1995); Kaasalainen+ (2001); West+ (2010); Knowles (2018); Denk and Mottola (2019); Mottola+ (2023)
(9) Links, references, acknowledgments
♦ Links outside
•Scott Sheppard (discovered a large number of Irregular moons): Saturn moons
•Wikipedia: 
Irregular moon 
Irregulärer Satellit
•Wikipedia: Moons of Saturn Liste der Saturnmonde
•Wikipedia: Naming of moons
•JPL (Jet Propulsion Laboratory): Solar System Dynamics HORIZONS Planetary Satellite Discovery Circumstances
•YouTube (JPL): 
Outer-moons dynamics (JPL’s Von-Kármán Lecture Series 17 Mar 2022)
•YouTube: Modern Major Moons — a song about names of 176 satellites (from 2015)
•MPC (Minor Planet Center): Natural Satellites Ephemeris Service
•David Jewitt (Sheppard’s former adviser): Irregular planetary satellites
•About naming Saturn’s Inuit moons (from Canadian Aboriginal Journal Windspeaker): jpg of article; text only website of article (last four paragraphs are missing on this website); pdf of complete Oct 2003 issue
•Discovery announcements: 2019 (Sheppard) • 2023 (Ashton/UBC) • 2023 (MPC Newsletter)
♦ Links inside (to conference contributions)
DPS 2018, ID 416.12 (Observations of Saturn’s Irregular moons): Abstract, Poster
♦ References (that include my work) (time-ordered)
 |
Denk, T., Mottola, S. (2019): Studies of Irregular Satellites: I. Lightcurves and Rotation Periods of 25 Saturnian Moons from Cassini Observations. Icarus 322, 80-103. doi:10.1016/j.icarus.2018.12.040 |
|
Denk, T., Mottola, S. (2019 LPSC): Cassini Observations of Saturn’s Irregular Moons. 50th LPSC conference, abstract #2654, The Woodlands, TX, 18−22 Mar 2019. |
|
Denk, T., Mottola, S., Tosi, F., Bottke, W.F., Hamilton, D.P. (2018): The Irregular Satellites of Saturn. In: Enceladus and the Icy Moons of Saturn (Schenk, P.M., Clark, R.N., Howett, C.J.A., Verbiscer, A.J., Waite, J.H., editors), Space Science Series, The University of Arizona Press, 409-434. |
|
Denk, T., Mottola, S. (2018 EPSC): Cassini Observations of Saturn’s Irregular Moons. European Planetary Science Congress, EPSC2018−103, Berlin, 16−21 Sep 2018. |
 |
◊ Denk, T., Mottola, S. (2013 DPG): Saturns äußerer Mond Ymir. DPG/AEF-Tagung, abstract EP 7.2, Jena, 28 Februar 2013. |
|
Jaumann, R., Clark, R.N., Nimmo, F., Hendrix, A.R., Buratti, B.J., Denk, T., Moore, J.M., Schenk, P.M., Ostro, S.J., Srama, R. (2009): Icy Satellites: Geological Evolution and Surface Processes. In: Saturn after Cassini-Huygens, Dougherty, M., Esposito, L., Krimigis, S. (eds.), Springer-Verlag, chapter 20, 637-681. |
|
Roatsch, Th., M. Wählisch, F. Scholten, A. Hoffmeister, K.-D. Matz, T. Denk, G. Neukum, P.C. Thomas, P. Helfenstein, C.C. Porco (2006): Mapping of the icy Saturnian satellites: First results from Cassini-ISS. Planetary and Space Science 54, 1137-1145. |
|
Giese, B., G. Neukum, Th. Roatsch, T. Denk, C.C. Porco (2006): Topographic modeling of Phoebe using Cassini images. Planetary and Space Science 54, 1156-1166. |
|
Porco, C.C., Baker, E., Barbara, J., Beurle, K., Brahic, A., Burns, J.A., Charnoz, S., Cooper, N., Dawson, D.D., DelGenio, A.D., Denk, T., Dones, L., Dyudina, U., Evans, M.W., Giese, B., Grazier, K., Helfenstein, P., Ingersoll, A.P., Jacobson, R.A., Johnson, T.V., McEwen, A.S., Murray, C.D., Neukum, G., Owen, W.M., Perry, J., Roatsch, T., Spitale, J., Squyres, S.W., Thomas, P.C., Tiscareno, M., Turtle, E.P., Vasavada, A.R., Veverka, J., Wagner, R., West, R. (2005): Cassini Imaging Science: Initial Results on Phoebe and Iapetus. Science 307, 1237-1242. |
♦ References (work from colleagues) (alphabet-ordered)
|
Ashton, E., Gladman, B., Beaudoin, M. (2021): Evidence for a Recent Collision in Saturn’s Irregular Moon Population. Planetary Science Journal 2:158 (12pp). |
|
Ashton, E., Gladman, B., Beaudoin, M., Alexandersen, M., Petit, J.-M. (2022): Discovery of the Closest Saturnian Irregular Moon, S/2019 S 1, and Implications for the Direct/Retrograde Satellite Ratio. Planetary Science Journal 3:107 (5pp). |
|
Bauer, J.M., Buratti, B.J., Simonelli, D.P., Owen, W.M. (2004): Recovering the rotational light curve of Phoebe. Astrophys. J. 610, L57-L60. |
|
Bauer, J.M., Grav, T., Buratti, B.J., Hicks, M.D. (2006): The phase curve survey of the irregular saturnian satellites: A possible method of physical classification. Icarus 184, 181-197. |
|
Bottke W.F., Nesvorný D., Vokrouhlický D., Morbidelli A. (2010): The irregular satellites: The most collisionally evolved population in the solar system. Astron. J. 139, 994-1014. |
|
Buratti, B.J., Hicks, M.D., Davies, A. (2005): Spectrophotometry of the small satellites of Saturn and their relationship to Iapetus, Phoebe, and Hyperion. Icarus 175, 490-495. [ Word of caution: Nomenclature is erroneously mixed in this paper. S/2000 S3 is (S29) Siarnaq, not (S21) Tarvos. S/2000 S11 is (S26) Albiorix, not (S29) Siarnaq. The four Irregulars observed for this work were Ymir, Paaliaq, Siarnaq, and Albiorix. In section 3.2 and Fig. 2, it is the lightcurve of (S29) Siarnaq which is discussed here — not (S21) Tarvos. ] |
|
Gomes-Júnior, A.R., Assafin, M., Braga-Ribas, F., Benedetti-Rossi, G., Morgado, E., Camargo, J.I.B., Vieira-Martins, R., Desmars, J., Sicardy, B., Barry, T., Campbell-White, J., Fernández-Lajús, E., Giles, D., Hanna, W., Hayamizu, T., Hirose, T., De Horta, A., Horvat, R., Hosoi, K., Jehin, E., Kerr, S., Machado, D.I., Mammana, L.A., Maybour, D., Owada, M., Rahvar, S., Snodgrass, C. (2020): The first observed stellar occultations by the irregular satellite Phoebe (Saturn IX) and improved rotational period. Month. Not. Roy. Astron. Soc. 492, 770-781. |
|
Grav, T., Bauer, J.M. (2007): A deeper look at the colors of the saturnian irregular satellites. Icarus 191, 267-285. |
|
Grav, T., Bauer, J.M., Mainzer, A.K., Masiero, J.R., Nugent, C.R., Cutri, R.M., Sonnett, S., Kramer, E. (2015): NEOWISE: Observations of the irregular satellites of Jupiter and Saturn. Astrophys. J. 809(3), 9 pp. |
|
Graykowski, A., Jewitt, D. (2018): Colors and Shapes of the Irregular Planetary Satellites. Astron. J. 155(184), 10 pp. |
|
Jacobson, R., Brozović, M., Gladman, B., Alexandersen, M., Nicholson, P.D., Veillet, C. (2012): Irregular satellites of the outer planets: Orbital uncertainties and astrometric recoveries in 2009–2011. Astron. J. 144:132, 8pp. |
|
Jacobson, R. (2022): The Orbits of the Main Saturnian Satellites, the Saturnian System Gravity Field, and the Orientation of Saturn’s Pole. Astron. J. 164:199, 19pp. |
|
Jacobson, R., Brozović, M., Mastrodemos, N., Riedel, J.E., Sheppard, S.S. (2022): Ephemerides of the Irregular Saturnian Satellites from Earth-based Astrometry and Cassini Imaging. Astron. J. 164:240, 10pp. |
|
Jewitt, D., Sheppard, S.S. (2005): Irregular Satellites in the Context of Planet Formation. Space Science Reviews 116, 441-455. |
|
Jewitt, D., Sheppard, S.S., Kleyna, J. (2006): The strangest satellites in the solar system. Scientific American 295, 40-47. |
|
Jewitt, D., Haghighipour, N. (2007): Irregular satellites of the planets: Products of capture in the early solar system. Annu. Rev. Astro. Astrophys. 45, 261-295. |
|
Kaasalainen, M., Torppa, J., Muinonen, K. (2001): Optimization Methods for Asteroid Lightcurve Inversion. II. The Complete Inverse Problem. Icarus 153, 37-51. |
|
Knowles, B. (2018): Cassini Imaging Science Subsystem (ISS) Data User’s Guide. pdf document, PDS (Planetary Data System) website, 179 pp. |
|
Mottola, S., De Angelis, G., Di Martino, M., Erikson, A., Hahn, G., Neukum, G. (1995): The Near‐Earth Objects Follow‐Up Program: First Results. Icarus 117, 62-70. |
|
Mottola, S., Hellmich, S., Buie, M.W., Zangari, A.M., Stephens, R.D., Di Martino, M., Proffe, G., Marchi, S., Olkin, C.B., Levison, H.F. (2023): Shape Models of Lucy Targets (3548) Eurybates and (21900) Orus from Disk-integrated Photometry. Planetary Science Journal 4:18 (20pp). |
|
Nesvorný, D., Vokrouhlický, D., Morbidelli, A. (2007): Capture of irregular satellites during planetary encounters. Astron. J. 133, 1962-1976. |
|
Nesvorný, D., Vokrouhlický, D., Deienno, R. (2014): Capture of irregular satellites at Jupiter. Astrophys. J. 784(22), 6 pp. |
|
Nicholson, P.D., Ćuk, M., Sheppard, S.S., Nesvorný, D., Johnson, T.V. (2008): Irregular satellites of the giant planets. In: The Solar System Beyond Neptune (Barucci, M.A. et al., eds.), Space Science Series, The University of Arizona Press, 411-424. |
|
Porco, C.C. West, R.A., Squyres, S.W., McEwen, A.S., Thomas, P.C., Murray, C.D., Del Genio, A., Ingersoll, A.P., Johnson, T.V., Neukum, G., Veverka, J., Dones, L., Brahic, A., Burns, J.A., Haemmerle, V., Knowles, B., Dawson, D., Roatsch, Th., Beurle, K., Owen, W. (2004): Cassini imaging science: Instrument characteristics and capabilities and anticipated scientific investigations at Saturn. Space Sci. Rev. 115, 363-497. |
|
Sheppard, S.S. (2006): Outer irregular satellites of the planets and their relationship with asteroids, comets and Kuiper belt objects. In: Asteroids, Comets, Meteors (ACM) (Lazzaro, D. et al., eds.), p. 319-334. IAU Symp. No. 229, Cambridge Univ. Press, Cambridge. |
|
Sheppard, S.S., Tholen, D.J., Alexandersen, M., Trujillo, C.A. (2023): New Jupiter and Saturn Satellites Reveal New Moon Dynamical Families. RNAAS 7, 100. |
|
Thomas, P.C., Tiscareno, M.S., Helfenstein, P. (2018): The Inner Small Satellites of Saturn and Hyperion. In: Enceladus and the Icy Moons of Saturn (Schenk, P.M., Clark, R.N., Howett, C.J.A., Verbiscer, A.J., Waite, J.H., editors), Space Science Series, The University of Arizona Press, 387-408. |
|
West, R.A., Knowles, B., Birath, E., Charnoz, S., Di Nino, D., Hedman, M., Helfenstein, P., McEwen, A., Perry, J., Porco, C.C., Salmon, J., Throop, H., Wilson, D. (2010): In-flight calibration of the Cassini imaging science sub-system cameras. Planet. Space Sci. 58, 1475-1488. |
♦ Acknowledgments
I am very grateful to the following institutions and persons without whom I would never have been able to conduct this work:
• Freie Universität (FU) Berlin — they managed the payment of my salary and business trips, and employed me from Oct 2003 until Dec 2019.
• DLR (Deutsches Zentrum für Luft- und Raumfahrt) in Berlin-Adlershof — they gave me leave to work at the FU and thus indirectly enabled me to work with Cassini throughout the whole mission from start to end; now (since Jan 2020), I’m back.
• DLR space administration in Bonn — they supported the Cassini work at FU through continuous third-party funding: absolutely critical.
• Cassini Project at JPL — it was a great pleasure and never a matter of course for me to work with such smart and kind people who navigated this “3½ billion dollar spaceship” throughout a really complicated path at multiple levels (means: from orbit dynamics through mission and science planning up to administrative tasks) (the latter is not an easy task when non-Americans have to be handled). My work was only possible because of the amazing work of hundreds (or were it even thousands?!) of engineers, scientists and staff who have dedicated their career to making this amazing mission possible and enabled me to do parts of the observation planning and the science. They deserve a lot of credit.
• Cassini Imaging team — great folks, same credits here; getting the task to do satellite imaging observation planning is among the best professional activity I can imagine.
• Stefano Mottola (DLR Berlin) — his outstanding expertise, dedicated software, inexhaustible patience and friendly nature were critical to the success of our attempts to ‘make sense of the data’.
• Thomas Roatsch (DLR Berlin) — he “piloted” the pdt software for our planning work throughout the mission; we spent hundreds (if not thousands) of hours to create and optimize the pointings of the Cassini observations of Dione, Rhea, Iapetus, and the Irregular moons.
• Heike Rosenberg (FU Berlin) — she provided critical information for the planning task (like the numbers used for the plots of all sheets “8B” and “8C” of each Irregular moon), and processed all ISS data of the mid-sized moons to produce image mosaics.
• Many others who are not explicitely mentioned here.
• Gerhard Neukum (DLR until 2002, then FU Berlin) — my original “gate” to the Cassini mission and even to planetary science: Without him, no Cassini for me.
© Tilmann Denk (2024)