← back to Outer Saturnian Moons
![]() Siarnaq is ∼39 kilometers (± 6 kilometers) in size and thus the largest prograde Irregular moon of Saturn. It has been discovered in 2000 joint with eleven other outer moons. Siarnaq’s mean distance to Saturn is ∼18 million kilometers, with one revolution around the planet on a prograde orbit requiring 2 years, 5 months and 1½ weeks. Siarnaq is a member of the Inuit group. At least four smaller moons share very similar orbital elements, indicating that Siarnaq is the largest surviver of a destructive collision aeons ago.
Siarnaq is ∼39 kilometers (± 6 kilometers) in size and thus the largest prograde Irregular moon of Saturn. It has been discovered in 2000 joint with eleven other outer moons. Siarnaq’s mean distance to Saturn is ∼18 million kilometers, with one revolution around the planet on a prograde orbit requiring 2 years, 5 months and 1½ weeks. Siarnaq is a member of the Inuit group. At least four smaller moons share very similar orbital elements, indicating that Siarnaq is the largest surviver of a destructive collision aeons ago.
From our Cassini measurements, the rotation period was determined to 10 h 11 min 16 sec. Siarnaq is thus the fastest rotator of all progradely orbiting satellites of Saturn (including the regular moons). The north pole of its rotation axis is only ~20° off the orbit plane of Saturn, indicating large seasonal variations on the surface. The convex-shape model shows a triangularly-shaped equatorial cross-section, and it might be possible that Siarnaq is a contact-binary “double” object.
Table of contents |
 |
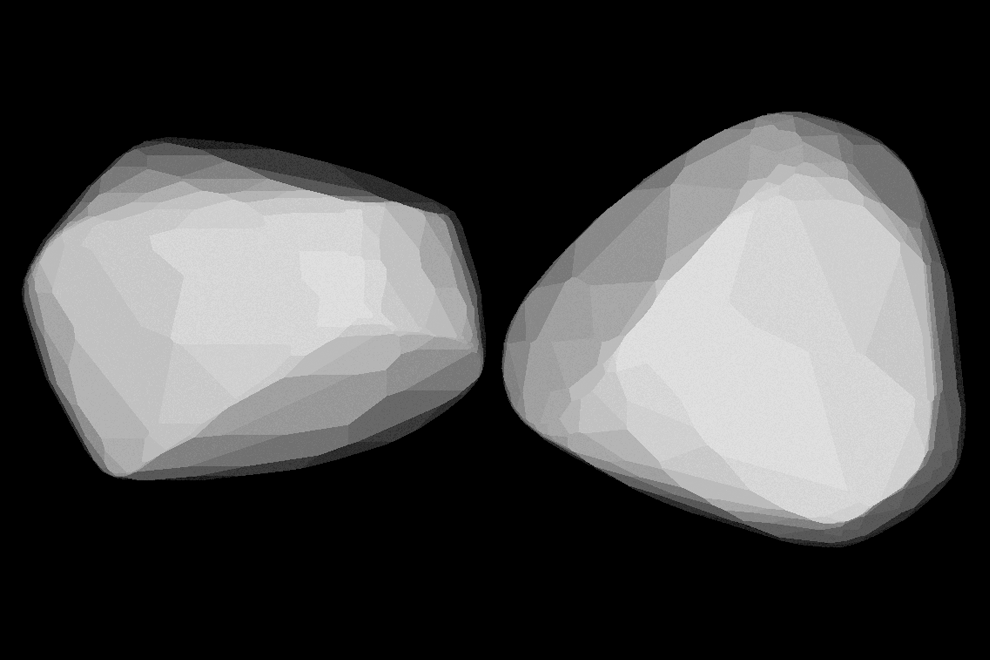 |
Fig. (middle): Three Cassini images of Siarnaq moving through constellation Lupus at a distance of 22 million kilometers during orbit 200. The images were calibrated, 3x zoomed, and cropped; the background stars were co-registered, the numerous cosmic ray hits in the original images were removed. Observation times (UTC): 30 Dec 2013 12:23 (red channel), 12:33 (green), 12:43 (blue). Same images as an animated-gif.
Fig. (right): Preliminary convex-shape model of Siarnaq (left: equatorial view, north up; right: north-pole view, rotated around the horizontal axis) (Fig. 3 in Denk et al. 2018).
This page is intended to compile (much of) our knowledge of Siarnaq in compact form. Its main focus will lie on the documentation of my Cassini-ISS work (observation planning and data analysis), but will also provide general information obtained from other work, like discovery circumstances and orbital and physical parameters. It will not include the raw data (images or spectra) taken by the Cassini spacecraft, these are available at NASA’s Planetary Data System (PDS). For further reading on Siarnaq and on Irregular moons of Saturn in general, see the reference list at my outer-Saturnian moons page.
This website is still in the early stages of development. As soon as papers will be reviewed or other information will be processed appropriately, more content will be added. I will remove this note when the page will be close to completion.
Last update: 19 May 2023 — page content is best displayed on a screen at least 1024 pixels wide
(1) Astronomical and physical properties
| Moon name | Saturn range | Orbit period | Orbit direction | Size | Rotation period | Discovery year |
| Siarnaq |
million km
|
years
|
prograde |
∼ km
|
h min
|
2000 |
Basic information about Siarnaq is offered in tabular form:
(1A) Designations and discovery circumstances
(1B) Orbit parameters
(1C) Physical parameters (body properties)
![]() ← Tables (1A) to (1C) in text format
← Tables (1A) to (1C) in text format
Most fundamental values are highlighted in red. The notes offer explanations, calculations, accuracies, references, etc. The data were obtained from spacecraft as well as from ground-based observations.
(1A) Designations and discovery circumstances
| Moon name(1) | Siarnaq | IAU number(3) | Saturn XXIX | First observation date(7) | 23 Sep 2000 | ||
| Moon abbrev. (TD)(2) | Sia | Provisional desig.(4) | S/2000 S 3 | Announcement date(7) | 25 Oct 2000 | ||
| SPICE ID(5) | 629 | IAU circ. announcement(7) | no. 7513 | ||||
| Also-used label(6) | S29 | Discoverers(8) | B. Gladman et al. |
Notes for Table 1A:
(1) Siarnaq’s name was announced on 08 Aug 2003 in IAU circ. 8177. It is named after a Siarnaq, a giantess in Inuit mythology who gave birth to the creatures of the sea. In different Inuit regions it has different names like Sedna, Talilajuk, Nuliajuk, or simply “the Old Woman Who Lives Down There”.
(2) I use this 3-letter abbreviation in the diagrams of my publications simply for practicability reasons. These have no offcial character.
(3) Moon numbers are assigned by the International Astronomical Union (IAU)’s Committee for Planetary System Nomenclature. For satellites, roman numeral designations are used.
(4) Designation given to the object in the first announcement; the guidelines are explained here.
(5) SPICE is a commonly-used information system of NASA’s Navigation and Ancillary Information Facility (NAIF). It assists engineers in modeling, planning, and executing planetary-exploration missions, and supports observation interpretation for scientists. Each planet and moon obtained a unique SPICE number.
(6) ‘S’ for ‘Saturnian moon’ plus the roman numeral designation in arabic numbers are often-used labels for satellites. Not sure how official that is.
(7) The date of the photography wherein the object was spotted for the first time is given in the IAU circular released on the announcement date.
(8) The discoverer team included: Brett Gladman, JJ Kavelaars, Jean-Marc Petit, Hans Scholl, Matthew Holman, Brian Marsden, Phil Nicholson, Joe Burns.
(1B) Orbit parameters
| Orbit direction(1) | prograde | Group member(2) | Inuit | Dynamical family(3) | Siarnaq | ||
| Periapsis range(4) | 13.09 ⋅ 106 km | Semi-major axis(5) | 18.182 ⋅ 106 km | Apoapsis range(6) | 23.27 ⋅ 106 km | ||
| Semi-major axis(7) | 301 R♄ | Semi-major axis(8) | 0.122 au | Semi-major axis(9) | 0.278 RHill | ||
| Orbit eccentricity(10) | 0.280 | Orbit inclination(11) | 45.8° | Inclination supplemental angle(12) | 45.8° | ||
| Orbital period(13) | 895.5 d | Orbital period(14) | 2 y 5 m 1½ w | Mean orbit velocity(15) | 1.44 km/s |
Notes for Table 1B:
(1) Prograde (counterclockwise as seen from north) or retrograde (clockwise as seen from north)
(3) Classification based on the a,e,i space in Fig. 1 and Table 2 in Denk et al. (2018)
(4) $r_{Peri}=a\cdot(1-e)$
(5) Orbit semi-major axis a, from JPL’s Solar System Dynamics Planetary Satellite Mean Elements website
(6) $r_{Apo}=a\cdot(1+e)$
(7) Saturn radius R♄ = 60330 km (100 mbar level)
(8) Astronomical Unit 1 au = 149 597 870.7 km
(9) Saturn’s Hill sphere radius $R_{Hill}=\sqrt[3]{m_♄/3m_☉}\cdot r_{♄↔☉}$ = ∼65 ⋅ 106 km = ∼1085 R♄ = ∼3° as seen from Earth at opposition (with mass of Saturn m♄ = 5.6836 ⋅ 1026 kg and perihel range Saturn↔Sun r♄↔☉ = 1.353 ⋅ 109 km)
(10) Orbit eccentricity e, from JPL’s Solar System Dynamics Planetary Satellite Mean Elements website
(11) Orbit inclination i, from JPL’s Solar System Dynamics Planetary Satellite Mean Elements website
(12) Orbit “tilt” or inclination supplemental angle i’ = i for prograde moons; i’ = 180°−i for retrograde moons
(13) From JPL’s Solar System Dynamics Planetary Satellite Mean Elements website
(14) Value from (13) in units of years, months, weeks
(15) $v=\sqrt{Gm_♄/a}$ (Gravitational constant G = 6.6741 ⋅ 10−20 km3 kg−1 s−2 )
(1C) Physical parameters
| Mean size(1) | 39 $^{+6}_{−6}$ km | Min. equatorial axes ratio(4) | 1.17 | Mass(6) | ∼ 1.6 ⋅ 1016 kg | ||
| Mean radius(2) | ∼ 19.7 km | Axes radii (a × b × c)(5) | tbd | Mean density(7) | 0.5 g/cm3 (?) | ||
| Equatorial circumference(3) | ∼ 130 km | Side lengths (equat. cross-sect.)(5) | tbd | Surface escape velocity(8) | ∼ 26 km/h | ||
| Rotation period (sidereal)(9) | 10.18785 h | +/- (9) | 0.00005 h | Spin rate(9) | 2.35575 d−1 | ||
| Spin direction(10) | lying on the side | Pole dir. (ecliptic longitude λ)(12) | 98°±15° | Pole direction (geocentric, RA)(13) | 97°±15° | ||
| Seasons(11) | extreme | Pole dir. (ecliptic latitude β)(12) | −23°±15° | Pole direction (geocentric, Dec)(13) | 0°±15° | ||
| Absolute visual magnitude(14) | ∼ 10.6 mag | Apparent vis. mag. from Earth(15) | 20.1 mag | Best apparent mag. for Cassini(16) | 10.8 mag | ||
| Spectral slope(17) | ∼ +13.0 %/100nm | B−R color index(17) | ∼ 1.36 | Albedo(18) | 0.06 (?) | ||
| Hill sphere radius(19) | ∼ 2900 km | Hill sphere radius(20) | ∼ 140 rSia |
(1) Determined by Grav et al. (2015) from NEOWISE data. Since it was determined from stacked images with an SNR ∼ 7, this diameter value is still uncertain.
(2) Half the diameter value. While the diameter is the intuitive size number, the radius r is mainly used in formulas to calculate other quantities. Important: While the given number is the formal result from the equation of note (1), the true precision is much lower (also see note (1)).
(3) Estimated under assumption of a circular equatorial circumference.
(4) Determined from the range between minima and maxima of a lightcurve obtained at low phase angle (from Table 3 in Denk et al. (2018)).
(5) Here, a is the long equatorial, b the short equatorial, and c the polar axis dimension of the reference ellipsoid. Since Siarnaq has a rather triangular cross-section, three equatorial side lengths are also given. These numbers were determined from the shape model.
(6) The mass is a very rough guess, estimated through density ρ and volume $\frac{4\pi}{3}r^3$; see notes (7) and (2).
(7) The density of Siarnaq is not known, the given number is speculative. There are indications from other Saturnian Irregular moons that these objects have quite low densities (well below 1 g/cm3), similar to comets or some of the inner small moons of Saturn. However, a higher density, maybe up to 2.5 g/cm3, cannot be ruled out.
(8) $v_{esc}=\sqrt{\frac{2GM}{R}}$; very rough guess as well since it depends on Siarnaq’s mass (note (6)) and radius (notes (1) and (2)) which are not well known. G = 6.674 · 1011 m3 kg−1 s−2 (Gravitational constant).
(9) Rotation period P and error determined with Cassini data; from Table 3 in Denk and Mottola (2018). See the lightcurves section below for details. The spin rate is 24/P, measured in units of one per day.
(10) Valid entries: Prograde (counterclockwise as seen from north), retrograde (clockwise as seen from north), ‘lying on the side’ (pole direction almost perpenticular to ecliptic pole), or ‘unknown’.
(11) Valid entries: “None” (rotation axis points close to one of the ecliptic poles), “moderate” (rotation axis is moderately tilted), or “extreme” (rotation axis is highly tilted, points somewhere close to the ecliptic equator), or ‘unknown’.
(12) From Cassini data (Denk et al. 2018). See the pole-direction sheet below for details.
(13) As (12), but in geocentric coordinates (Right Ascension and Declination).
(14) From Table 2 in Denk et al. (2018); the number may be uncertain by several tenths of magnitude. The absolute visual magnitude HV is the magnitude (brightness) of an object (in the visible wavelength range) if located 1 au away from the sun and observed at 0° phase angle (i.e., in this definition, the observer virtually sits at the center of the sun). The magnitude scale is logarithmic, with an object of 6th mag being 100x darker than a 1st mag object.
(15) Apparent visual magnitude V; from Table 2 in Denk et al. (2018).
(16) From Table 2 in Denk and Mottola (2018). Given is the best apparent magnitude as seen from Cassini at a time when an observation took place.
(17) Color information: Mean spectral slope S’2 is from Table 3 in Grav and Bauer (2007), the B−R color index is from the same paper. The higher the value, the “redder” the color of the object. Mean wavelengths: 445 nm for B (“blue”), 658 nm for R (“red”) filters. B−R of the Sun is 1.01 (Ramírez et al. 2012).
(18) Might vary by ±0.03; see discussions in Grav et al. (2015) and Denk et al. (2018).
(19) Hill radius at periapsis under the assumption of the given density (see note (7)). The number would be larger for a higher density, or lower for a lower density.
(20) Hill radius at periapsis in Siarnaq-radius units. With $R_{Hill}=\sqrt[3]{4\pi\rho_{Sia}/9m_♄}\cdot r_{Sia↔♄}$, this number only depends on the object’s distance to the central body (Saturn; linear dependency) and on the object’s density (proportional to the cubic root; see also note (7)).
© Tilmann Denk (2023)