← back to ‘Outer Moons of Saturn’
![]() Aegir is ∼5 kilometers in size and thus a “mid-sized” Irregular moon of Saturn. It has been discovered in 2004 joint with eleven other outer moons. Aegir’s mean distance to Saturn is ∼21 million kilometers, with one revolution around the planet on a retrograde orbit requiring 3 years and 3 weeks.
Aegir is ∼5 kilometers in size and thus a “mid-sized” Irregular moon of Saturn. It has been discovered in 2004 joint with eleven other outer moons. Aegir’s mean distance to Saturn is ∼21 million kilometers, with one revolution around the planet on a retrograde orbit requiring 3 years and 3 weeks.
Since Aegir’s ephemeris (position in the sky) was not accurately known at that time, we did not make an attempt to observe it with Cassini. The best chance would have been in early spring 2015, but due to competition with other objects and due to the uncertain ephemeris, we did not try.
Table of contents(1) Astronomical and physical properties |
 |
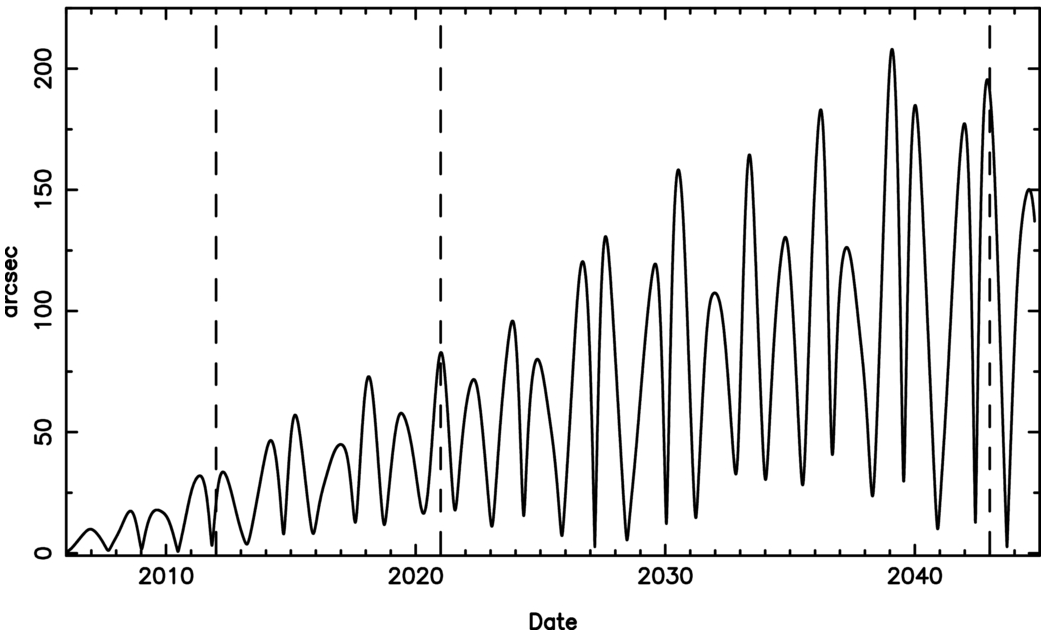 |
Fig. (middle): Since no Cassini image of Aegir exists, a fictive drawing of Aegir, taken from Karley Sullivan’s Satellite Hand drawings on the MOCAM website, is used here for illustration and fun.
Fig. (right): Time history of the on-sky position uncertainty for Aegir as seen from Earth (Fig. 1 from Jacobson et al. 2012). In the mean time, with observation campaigns from 2019 to 2021, Aegir’s orbit is safe (Jacobson et al. 2022).
This page compiles (much of) our knowledge of Aegir in compact form. It provides general information like discovery circumstances and orbital and physical parameters, plus viewing geometries from the Cassini spacecraft. For further reading on Aegir and on Irregular moons of Saturn in general, see the reference list at my ‘Outer Moons of Saturn’ page.
Last update: 20 May 2023 — page content is best displayed on a screen at least 1024 pixels wide
(1) Astronomical and physical properties
| Moon name | Saturn range | Orbit period | Orbit direction | Size | Rotation period | Discovery year |
| Aegir |
million km
|
years
|
retrograde |
∼ km
|
unknown
|
2004 |
Basic information about Aegir is offered in tabular form:
(1A) Designations and discovery circumstances
(1B) Orbit parameters
(1C) Physical parameters (body properties)
![]() ← Tables (1A) to (1C) in text format
← Tables (1A) to (1C) in text format
Most fundamental values are highlighted in red. The notes offer explanations, calculations, accuracies, references, etc. The data were obtained from ground-based observations.
(1A) Designations and discovery circumstances
| Moon name(1) | Aegir | IAU number(3) | Saturn XXXVI | First observation date(7) | 12 Dec 2004 | ||
| Moon abbrev. (TD)(2) | Aeg | Provisional designation(4) | S/2004 S 10 | Announcement date(7) | 04 May 2005 | ||
| SPICE ID(5) | 636 | IAU circ. announcement(7) | no. 8523 | ||||
| Also-used label(6) | S36 | Discoverers(8) | S. Sheppard et al. |
Notes for Table 1A:
(1) Aegir’s name was announced on 05 Apr 2007 in IAU circ. 8826. It is taken from the Norse mythology where Ægir is a sea Jötunn who soothes storms away.
(2) I use this 3-letter abbreviation in the diagrams of my publications simply for practicability reasons. These have no offcial character.
(3) Moon numbers are assigned by the International Astronomical Union (IAU)’s Committee for Planetary System Nomenclature. For satellites, roman numeral designations are used.
(4) Designation given to the object in the first announcement; the guidelines are explained here.
(5) SPICE is a commonly-used information system of NASA’s Navigation and Ancillary Information Facility (NAIF). It assists engineers in modeling, planning, and executing planetary-exploration missions, and supports observation interpretation for scientists. Each planet and moon obtained a unique SPICE number.
(6) ‘S’ for ‘Saturnian moon’ plus the roman numeral designation in arabic numbers are often-used labels for satellites. Not sure how official that is.
(7) The date of the photography wherein the object was spotted for the first time is given in the IAU circular released on the announcement date.
(8) The discoverer team included: Scott Sheppard, David Jewitt, and Jan Kleyna.
(1B) Orbit parameters
| Orbit direction(1) | retrograde | Group member(2) | Norse | Dynamical family(3) | Mundilfari | ||
| Periapsis range(4) | 15.52 ⋅ 106 km | Semi-major axis(5) | 20.751 ⋅ 106 km | Apoapsis range(6) | 25.98 ⋅ 106 km | ||
| Semi-major axis(7) | 344 R♄ | Semi-major axis(8) | 0.139 au | Semi-major axis(9) | 0.317 RHill | ||
| Orbit eccentricity(10) | 0.252 | Orbit inclination(11) | 166.7° | Inclination supplemental angle(12) | 13.3° | ||
| Orbital period(13) | 1120.6 d | Orbital period(14) | 3 y 0 m 3¼ w | Mean orbit velocity(15) | 1.35 km/s |
Notes for Table 1B:
(1) Prograde (counterclockwise as seen from north) or retrograde (clockwise as seen from north)
(3) Classification based on the a,e,i space in Fig. 1 and Table 2 in Denk et al. (2018)
(4) $r_{Peri}=a\cdot(1-e)$
(5) Orbit semi-major axis a, from JPL’s Solar System Dynamics Planetary Satellite Mean Elements website
(6) $r_{Apo}=a\cdot(1+e)$
(7) Saturn radius R♄ = 60330 km (100 mbar level)
(8) Astronomical Unit 1 au = 149 597 870.7 km
(9) Saturn’s Hill sphere radius $R_{Hill}=\sqrt[3]{m_♄/3m_☉}\cdot r_{♄↔☉}$ = ∼65 ⋅ 106 km = ∼1085 R♄ = ∼3° as seen from Earth at opposition (with mass of Saturn m♄ = 5.6836 ⋅ 1026 kg and perihel range Saturn↔Sun r♄↔☉ = 1.353 ⋅ 109 km)
(10) Orbit eccentricity e, from JPL’s Solar System Dynamics Planetary Satellite Mean Elements website
(11) Orbit inclination i, from JPL’s Solar System Dynamics Planetary Satellite Mean Elements website
(12) Orbit “tilt” or inclination supplemental angle i’ = i for prograde moons; i’ = 180°−i for retrograde moons
(13) From JPL’s Solar System Dynamics Planetary Satellite Mean Elements website
(14) Value from (13) in units of years, months, weeks
(15) $v=\sqrt{Gm_♄/a}$ (Gravitational constant G = 6.6741 ⋅ 10−20 km3 kg−1 s−2 )
(1C) Physical parameters
| Mean size(1) | 4½ $^{+1½}_{−½}$ km | Min. equatorial axes ratio(4) | unknown | Mass(6) | ∼ 2 ⋅ 1013 kg | ||
| Mean radius(2) | ∼ 2.2 km | Axes radii (a × b × c)(5) | unknown | Mean density(7) | 0.5 g/cm3 (?) | ||
| Equatorial circumference(3) | ∼ 15 km | Surface escape velocity(8) | ∼ 3 km/h | ||||
| Rotation period(9) | unknown | +/- (9) | — | Spin rate(9) | unknown | ||
| Spin direction(10) | unknown | Pole dir. (ecliptic longitude λ)(12) | unknown | Pole direction (geocentric, RA)(13) | unknown | ||
| Seasons(11) | unknown | Pole dir. (ecliptic latitude β)(12) | unknown | Pole direction (geocentric, Dec)(13) | unknown | ||
| Absolute visual magnitude(14) | ∼ 15.5 mag | Apparent vis. mag. from Earth(15) | 24.4 mag | Best apparent mag. for Cassini(16) | 15.8 mag | ||
| B−R color index(17) | 1.30 | Albedo(18) | 0.06 (?) | ||||
| Hill sphere radius(19) | ∼ 360 km | Hill sphere radius(20) | ∼ 165 rAeg |
(1) Determined from absolute visual magnitude H (see note (14)). The conversion from H to size (diameter of a reference sphere) was calculated through $D=1 \text{ au}\cdot \frac{2}{\sqrt{A}}\cdot 10^{−0.2·(H−M_☉)}$; with solar apparent V magnitude M☉ = −26.71 ± 0.02 mag and Astronomical Unit 1 au = 149 597 870.7 km. For Aegir’s albedo, see note (18). Due to the uncertain input values, a size determined this way may be uncertain to ∼ −15/+30% (for A ± 0.02 and H ± 0.1).
(2) Half the diameter value. While the diameter is the intuitive size number, the radius r is mainly used in formulas to calculate other quantities. Important: While the given number is the formal result from the equation of note (1), the true precision is much lower (also see note (1)).
(3) Estimated under assumption of a circular equatorial circumference.
(4) Ratio between long equatorial reference axis a and short equatorial reference axis b; unknown because no lightcurve is available.
(5) Unknown because no shape model is available.
(6) The mass is a very rough guess, estimated through density ρ and volume $\frac{4\pi}{3}r^3$; see notes (7) and (2).
(7) The density of Aegir is not known, the given number is speculative. There are indications from other Saturnian Irregular moons that these objects have quite low densities (well below 1 g/cm3), similar to comets or some of the inner small moons of Saturn. However, a higher density, maybe up to 2.5 g/cm3, cannot be ruled out.
(8) $v_{esc}=\sqrt{\frac{2GM}{R}}$; very rough guess as well since it depends on Aegir’s mass (note (6)) and radius (notes (1) and (2)) which are not well known. G = 6.674 · 1011 m3 kg−1 s−2 (Gravitational constant).
(9) Unknown because Cassini could not observe the object.
(10) Valid entries: Prograde (counterclockwise as seen from north), retrograde (clockwise as seen from north), ‘lying on the side’ (pole direction almost perpenticular to ecliptic pole), or ‘unknown’.
(11) Valid entries: “None” (rotation axis points close to one of the ecliptic poles), “moderate” (rotation axis is moderately tilted), or “extreme” (rotation axis is highly tilted, points somewhere close to the ecliptic equator), or ‘unknown’.
(12) —
(13) —
(14) From Table 2 in Denk et al. (2018); the number may be uncertain by several tenths of magnitude. The absolute visual magnitude H is the magnitude (brightness) of an object (in the visible wavelength range) if located 1 au away from the sun and observed at 0° phase angle (i.e., in this definition, the observer virtually sits at the center of the sun). The magnitude scale is logarithmic, with an object of 6th mag being 100x darker than a 1st mag object.
(15) Apparent visual magnitude V; from Table 2 in Denk et al. (2018).
(16) From Table 2 in Denk et al. (2018) (but no observations were performed).
(17) Color information: B−R color index: From Graykowski and Jewitt (2018). The higher the value, the “redder” the color of the object. Mean wavelengths: 445 nm for B (“blue”), 658 nm for R (“red”) filters. B−R of the Sun is 1.01 (Ramírez et al. 2012).
(18) Might vary by ±0.03 or even more; see discussion in Denk et al. (2018).
(19) Hill radius at periapsis under the assumption of the given density (see note (7)). The number would be larger for a higher density, or lower for a lower density.
(20) Hill radius at periapsis in Aegir-radius units. With $R_{Hill}=\sqrt[3]{4\pi\rho_{moon}/9m_♄}\cdot r_{moon↔Saturn}$, this number only depends on the object’s distance to the central body (Saturn; linear dependency) and on the object’s density (proportional to the cubic root; see also note (7)).
(8) Cassini view
Table of contents:
(8B) Map: Aegir in the sky of Cassini
(8C) Aegir geometry and visibility graph (range, phase, and magnitude vs. time)
The Cassini spacecraft made no attempt to observe Aegir.
(8B) Map: Aegir in the sky of Cassini
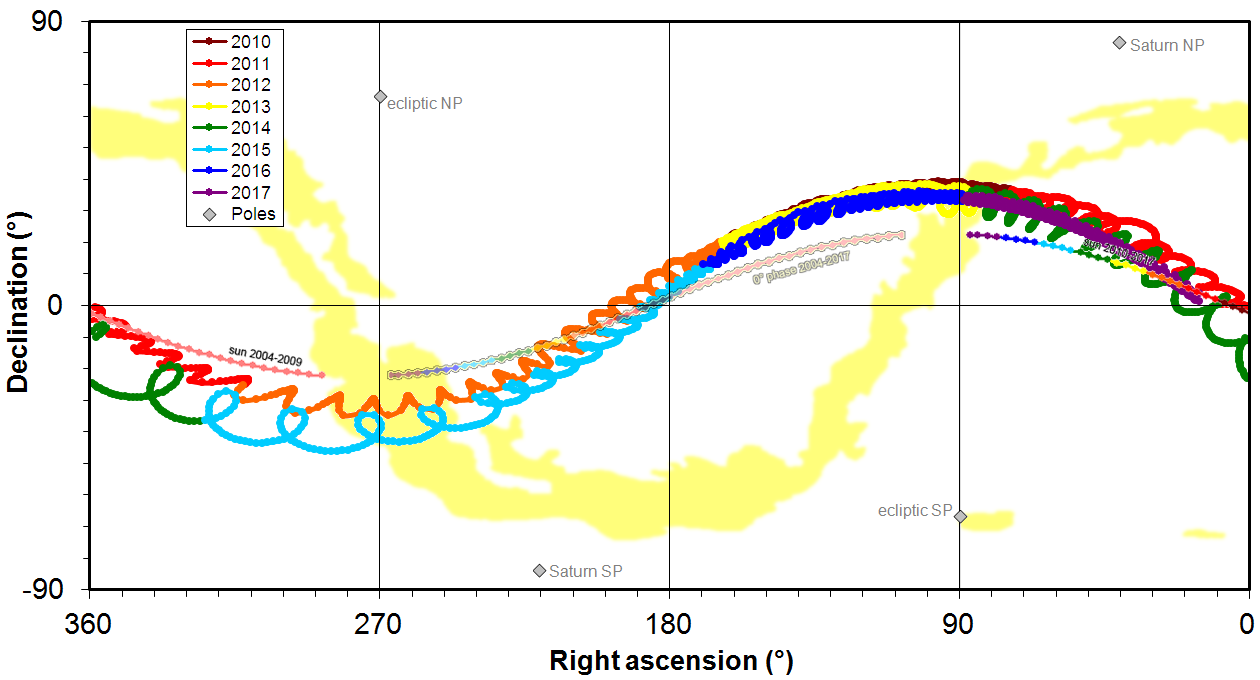 Aegir as visible to Cassini between 2010 and 2017. Orthographic projection of the sky; geocentric coordinate system (RA/Dec). As a retrograde object, Aegir moves from left to right.
Aegir as visible to Cassini between 2010 and 2017. Orthographic projection of the sky; geocentric coordinate system (RA/Dec). As a retrograde object, Aegir moves from left to right.
Shown are Aegir’s locations (colored, wiggled lines), the location of the sun from 2004 to 2017 (smooth sinusoidal line from RA ∼ 290° to ∼ 85°; the sun moves from right to left), the location of the anti-sun (0° phase) from 2004 to 2017 (pale sinusoidal line from RA ∼ 110° to ∼ 265°), the Milky Way (yellow band) and the Magellanic clouds (yellow spots to the lower right), the ecliptic poles (gray diamonds), and Saturn’s poles (gray diamonds).
NP = north pole; SP = south pole.
(8C) Aegir geometry and visibility graph
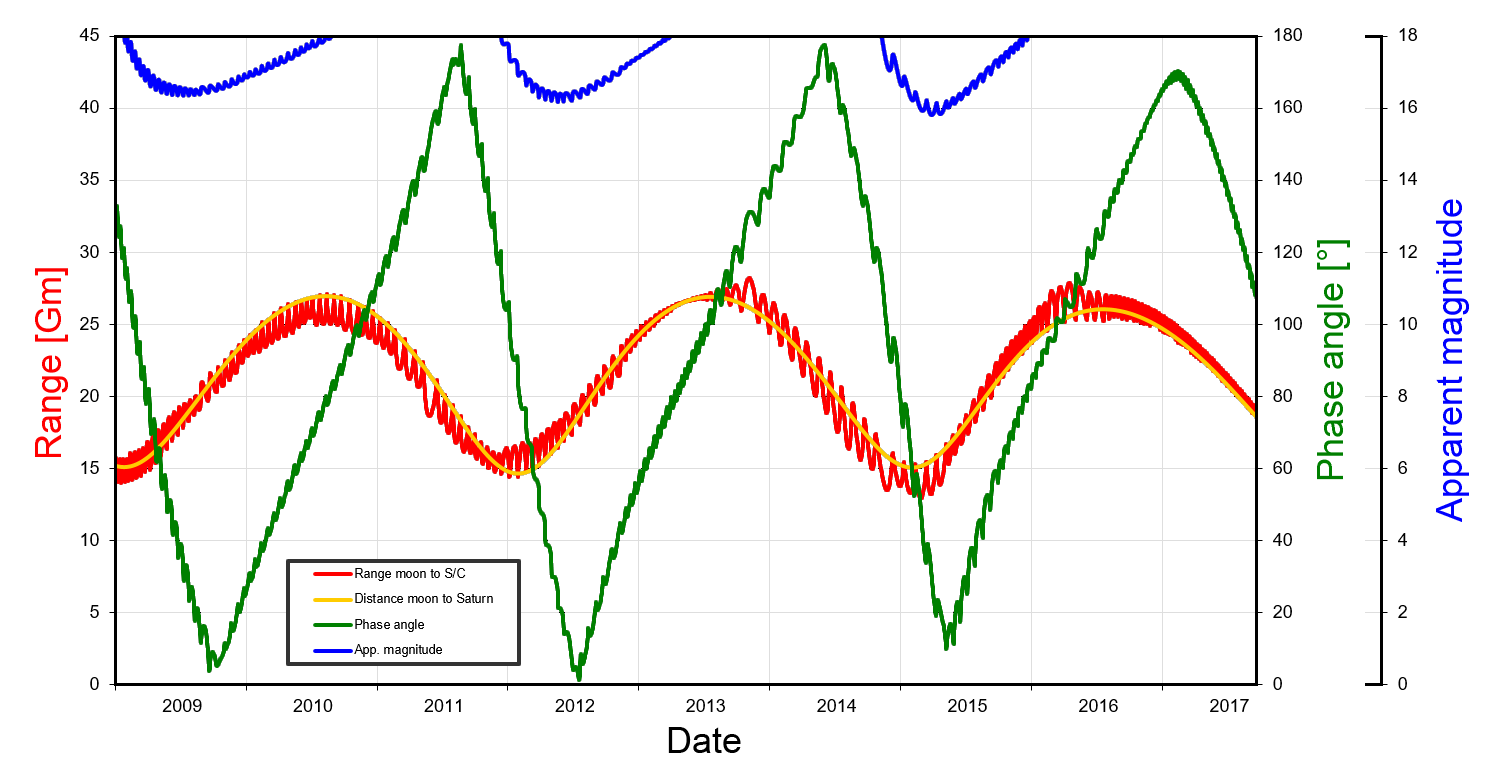 This graph has been used to seek for potential Aegir observation opportunities.
This graph has been used to seek for potential Aegir observation opportunities.
Notes: Left axis: Range of Aegir to Cassini (red) and to Saturn (orange); right axes: phase angle (green) and apparent magnitude of Aegir (blue) as seen from Cassini for the time range 01 Jan 2009 to 15 Sep 2017 (end-of-mission).
(9) References for Aegir
IAU circular, discovery: no. 8523
IAU circular, naming: no. 8826
Wikipedia: ![]() Aegir (moon)
Aegir (moon) ![]() Aegir (Mond)
Aegir (Mond)
My ‘Outer Moons of Saturn’ website: Sheet ‘links and references’
| Denk, T., Mottola, S., Tosi, F., Bottke, W.F., Hamilton, D.P. (2018): The Irregular Satellites of Saturn. In: Enceladus and the Icy Moons of Saturn (Schenk, P.M., Clark, R.N., Howett, C.J.A., Verbiscer, A.J., Waite, J.H., editors), Space Science Series, The University of Arizona Press, pp. 409-434. | |
| Jacobson, R., Brozović, M., Gladman, B., Alexandersen, M., Nicholson, P.D., Veillet, C. (2012): Irregular satellites of the outer planets: Orbital uncertainties and astrometric recoveries in 2009–2011. Astron. J. 144(132), 8 pp. | |
| Jacobson, R., Brozović, M., Mastrodemos, N., Riedel, J.E., Sheppard, S.S. (2022): Ephemerides of the Irregular Saturnian Satellites from Earth-based Astrometry and Cassini Imaging. Astron. J. 164:240, 10pp. |
© Tilmann Denk (2023)